بررسی مقالات مرتبط با زنجیره تأمین خون - بررسی مقاله نهم

موضوع:

مدیریت موجودی پلاکت‌ها در زنجیره تأمین خون با هدف حداقل کردن سطح کمبود و اتلاف

چکیده:

بیمارستان‌ها و مراکز خونی به دلیل طول عمر اندک پلاکت‌ها و عدم‌قطعیت در تقاضا، سطح بالایی از کمبود و اتلاف را تجربه می‌کنند. بدین منظور، برخورداری از یک مدل موجودی مناسب در بیمارستان‌ها و مراکز خونی امری ضروری است. در این مقاله، یک مدل برنامه‌ریزی احتمالی تحت شرایط عدم‌قطعیت تقاضا توسعه داده شده‌است که سیاست‌های سفارش‌دهی را در طول زنجیره تأمین تعیین می‌کند. برای حل این مدل در ابعاد بزرگ، یک الگوریتم ژنتیک توسعه‌داده‌شده به نام الگوریتم ژنتیک احتمالی اصلاح‌شده (MSGA) ارائه شده‌است که عملکرد این الگوریتم با سایر الگوریتم‌های موجود مقایسه شده‌است و برای ارزیابی عملکرد مدل نیز، از یک مطالعه موردی استفاده شده‌است.  

مقدمه:

فسادپذیری فرآورده‌های خونی و عمر محدود آن‌ها، مدیریت موجودی خون را به امری پیچیده تبدیل کرده‌است. خون از چهار جزء اصلی تشکیل شده‌است: گلبول‌های قرمز، گلبول‌های سفید، پلاسما و پلاکت. با توجه به این که هر کدام از این فرآورده‌ها، کاربردهای خاصی در درمان بیماران دارند، بنابراین نگه‌داری هر یک از این فرآورده‌ها به مقدار کافی در بیمارستان‌ها و مراکز خون ضروری به نظر می‌رسد. چالش اصلی در نگه‌داری این محصولات، طول عمر کوتاه آن‌هاست. گلبول‌های قرمز و پلاسما دارای طول عمر نسبتاً طولانی‌تری هستند و به ترتیب دارای عمری چهل‌‌ودو روزه و یک‌ساله هستند؛ در حالی که عمر پلاکت بسیار کوتاهی و در حدود پنج روز است. گزارشها گویای آن است که حدود بیست درصد پلاکت‌های جمع‌آوری‌شده به دلیل سپری شدن دوره عمر آن‌ها، اتلاف می‌شوند.

زنجیره تأمین خون شامل فرآیندهای جمع‌آوری خون از اهداکنندگان، فرآوری آ‌ن‌ها و ارسال آن‌ها به بیمارستان‌ها برای برآورد تقاضای بیماران است. خون‌هایی که در محل‌های مختلف جمع‌آوری می‌شوند، 4-6 ساعت بعد از خون‌گیری به مراکز خون فرستاده می‌شوند. در این مراکز، خون به انواع فرآورده‌های خونی تجزیه می‌شود و سپس، جهت اطمینان از سلامت خون‌های اهداشده از عفونت‌ها و انواع بیماری‌ها، آزمایش می‌شوند. بعد از این مرحله که تقریباً حدود دو روز به طول می‌انجامد، واحدهای خونی سالم برای مصارف درمانی به بیمارستان‌ها و مراکز جراحی منتقل می‌شوند.

تقاضاهای خونی با گذشت زمان، به دلایلی نظیر افزایش جراحی‌ها و سالخوردگی جمعیت در حال افزایش است و پیش‌بینی شده‌است که نرخ تقاضا، سالانه 4-5 درصد افزایش خواهد یافت. این در حالی است که تنها حدود 5 درصد از افراد جامعه به اهدای خون اقدام می‌کنند و به دلیل این محدودیت در عرضه خون، مراکز خون و بیمارستان‌ها با کمبود خون مواجه می‌شوند. کمبود خون باعث به تعویق افتادن جراحی‌ها در بیمارستان‌ها می‌شوند که عواقبی نظیر به خطر افتادن سلامتی بیماران و اختلال در برنا‌مه‌ریزی بیمارستان‌ها را به دنبال دارد.  

در حالی که در بیمارستان‌ها کمبود خون رخ می‌دهد، از سویی دیگر تعداد زیادی از واحدهای خونی، به‌خصوص پلاکت‌ها، اتلاف می‌شوند که این اتلاف خون ناشی از نامنظم و غیرقابل‌پیشبینی بودن تقاضا و طول عمر محدود فرآ‌ورده‌های خونی است. در آمریکا و کشورهای اروپایی حدود 20 درصد از پلاکت‌های جمع‌آوری‌شده اتلاف می‌شود که این درصد در کشورهای در حال توسعه بیشتر است. به دلیل عرضه محدود خون و حجم بالای اتلاف خون، عدم تطابق در عرضه و تقاضا ایجاد می‌شود که باعث افزایش هزینه‌های زنجیره تأمین خون می‌گردد. بنابراین با توجه به موارد مذکور، در این مقاله یک مدل موجودی به‌ منظور کاهش در اتلاف و کمبود پلاکت‌ها توسعه داده شده‌است که در آن تقاضا غیرقطعی و عرضه خون، محدود در نظر گرفته شده‌است.

ویژگی‌های اصلی مسئله:

·         توسعه یک مدل برنامه‌ریزی احتمالی برای مدیریت موجودی در یک زنجیره تأمین دوسطحی شامل مرکز خون و بیمارستان‌ها تحت شرایط عدم‌قطعیت تقاضا.

·         در نظر گرفتن دو نوع تقاضا، تقاضای معمولی و تقاضای اورژانسی، که برای برآورد تقاضاهای معمولی سفارشی از سوی بیمارستان‌ها در طول دوره‌های مرور موجودی صادر می‌شوند؛ ولی تقاضاهای اورژانسی زمانی رخ می‌دهد که بیمارستانی با کمبود مواجه شود.

·         ارائه الگوریتم ژنتیک توسعه‌یافته برای حل مدل در ابعاد بزرگ.

بیان مسئله:

ساختار یک زنجیره تأمین خون با یک مرکز خون و j بیمارستان در شکل 1 نشان داده شده‌است. با توجه به قانون نظام سلامت آمریکا، انتقال خون بین بیمارستان‌ها مجاز نیست که از این رو، در این مقاله نیز امکان انتقال خون بین بیمارستان‌ها وجود ندارد. 

شکل1. ساختار زنجیره تأمین خون ارائه‌شده در این مقاله

پلاکت‌های جمع‌آوری‌شده در بیمارستان‌ها و مراکز خون، در دستگاه‌های آژیتاتور (همزن) نگه‌داری می‌شود تا شرایط مناسب برای نگه‌داری آن‌ها فراهم شود. آژیتاتورها قادر به نگه‌داری تعداد محدودی از واحدهای پلاکت هستند و در مدل‌های موجودی این محدودیت فضا باید لحاظ گردد. بنابراین، در این مقاله از سیاست سفارش‌‌دهی (s,S) در بیمارستان‌ها و مراکز خون استفاده شده‌است. با به‌کارگیری این سیاست، در هر دوره مرور، موقعیت موجودی (موقعیت موجودی برابر است با حاصل‌جمع موجودی دردست و سفارش‌هایی که هنوز تحویل بیمارستان‌ها یا مراکز خون نشده‌اند) بررسی می‌شود و در صورتی که کمتر از s باشد، سفارشی صادر می‌شود تا موقعیت موجودی به S برسد و اگر موقعیت موجودی برابر یا بیشتر از نقطه سفارش مجدد (s) باشد، هیچ پلاکتی سفارش داده نمی‌شود.

با توجه به مقادیر مختلف تقاضاها، سناریوهای مختلفی در نظر گرفته‌ شده‌است که پارامترهای سفارش‌دهی (s,S) برای همه سناریوها یکسان است؛ ولی تعداد واحدهای سفارش‌ها، میزان اتلاف و کمبود خون و سطح موجودی خون در سناریوهای مختلف متفاوت است. محدودیت‌ها نیز برای سناریوهای مختلف تقاضا تغییر می‌کند و تابع هدف نیز، به دنبال حداقل کردن هزینه‌های کل مربوط به همه سناریوها است.

در شکل 2 و 3، به ترتیب فرآیندهای صورت‌گرفته در بیمارستان‌ها و مراکز خونی با جزئیات بیشتری نمایش داده ‌شده‌اند.

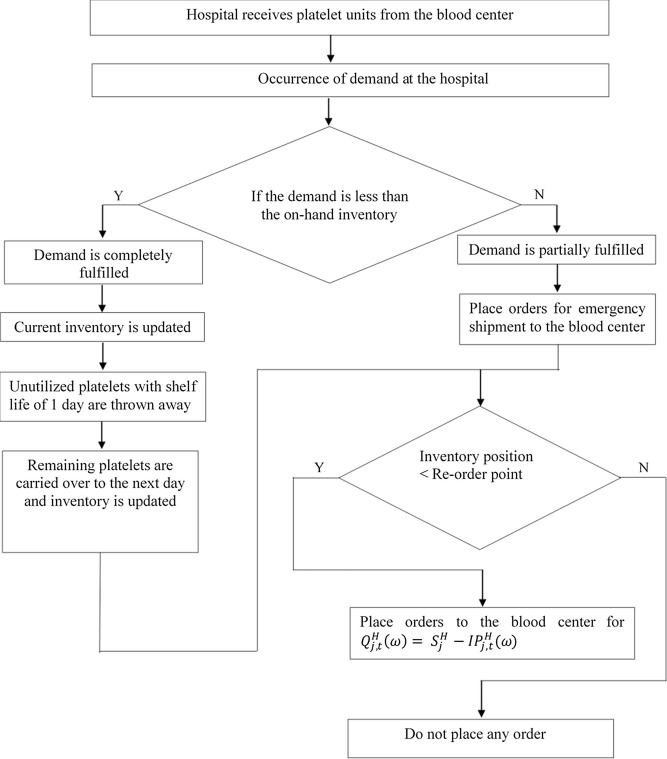
شکل2. عملیات‌های انجام‌شده در بیمارستان‌ها

 

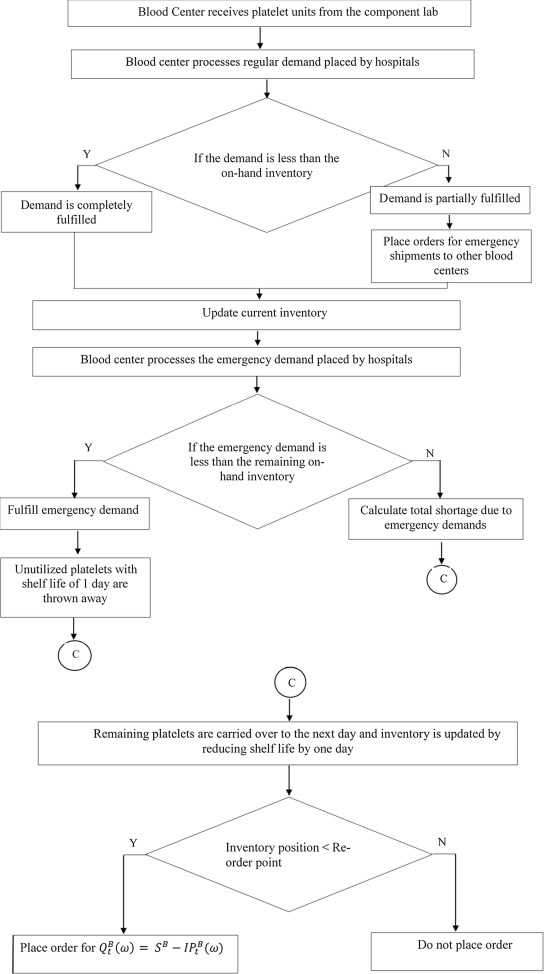
شکل3. عملیات‌های انجام‌شده در مرکز خون

مفروضات:

·         فرآورده‌های خونی بعد از انجام آزمایش، بلافاصله به مراکز خون فرستاده می‌شوند و بنابراین، پلاکت‌ها در این مراکز ، دارای طول عمر سه‌روزه هستند.

·         طول عمر پلاکت‌هایی که از مراکز خون به بیمارستان‌ها منتقل می‌شوند، تابعی از یک توزیع گسسته معین است که از الگوی داده‌های قبلی پیروی می‌کند.

·         مدل برای یک گروه خونی خاص ارائه شده‌است.

·         سیاست اعمال‌شده در بیمارستان‌ها و مرکز خون، سیاست FIFO است.

توالی عملیات روزانه در بیمارستان‌ها و مراکز خون:

1.       بیمارستان در ابتدای روز، سفارش‌های صادرشده در دوره‌های قبل را از مراکز خون دریافت می‌کند.

2.       بیمارستان تقاضاها را از سوی بیماران دریافت می‌کند.

3.       اگر تقاضاها بیشتر از موجودی در دست باشد، بخشی از تقاضاها توسط ذخایر موجود برطرف می‌شود.

4.       اگر تقاضاها کمتر از موجودی در دست باشند، تقاضاها طبق سیاست FIFO پاسخ داده می‌شوند و پس از ارضای تقاضاها، پلاکت‌های باقی‌مانده با طول عمر یک روز دورریز می‌شوند و پلاکت‌ها با طول عمر دو و سه روز، به موجودی روز بعد منتقل می‌‌شوند.

5.       در پایان هر دوره مرور، بیمارستان موقعیت موجودی خود را بررسی می‌کند. اگر موقعیت موجودی کمتر یا برابر نقطه سفارش مجدد باشد (s)، سفارش برای پلاکت صادر می‌شود تا سطح موجودی به S برسد که این سفارش بعد از سپری شدن مدت تحویل، به بیمارستان می‌رسد. در غیر این صورت، سفارشی صادر نمی‌شود.

توالی عملیات روزانه در یک مرکز خون و تحت هر سناریو:

1.       پلاکت تازه با طول عمر سه روز از آزمایشگاه به مرکز خون می‌رسد.

2.       مرکز خون تقاضاهای بیمارستان‌ها را بررسی می‌کند. این نوع تقاضاها، تقاضاهای معمولی نامیده می‌شوند.

3.       اگر مجموع تقاضاهای معمولی دریافت‌شده از بیمارستان‌ها بیشتر از موجودی در دست مرکز خون باشد، بخشی از تقاضاها از طریق ذخایر موجود برطرف می‌شوند. باقی تقاضاها، از سایر مراکز و به صورت اورژانسی تهیه می‌شوند که هزینه‌های اضافی به دنبال دارند. اگر مجموع تقاضاها کمتر از موجودی در دست باشند، طبق سیاست FIFO تقاضاها ارضا می‌شوند و موجودی به‌روز می‌شود.

4.       اگر در بیمارستانی کمبود رخ دهد، بیمارستان سفارشی مخصوص برای مرکز خون صادر می‌کند که باید فوراً توسط مرکز خون پاسخ داده‌شود. این تقاضا، تقاضای اورژانسی نامیده می‌شود. فرض شده‌است که تقاضای اورژانسی از طریق موجودی‌هایی پاسخ داده می‌شود که بعد از ارضای تقاضای معمولی در مرکز خون باقی مانده‌است.

5.       اگر تقاضای اورژانسی بیشتر از موجودی در دست مرکز خون باشد، بخشی از تقاضای اورژانسی توسط ذخایر موجود پاسخ داده می‌شود و تقاضاهای پاسخ داده‌نشده، هزینه کمبود را بر آن مرکز خونی تحمیل کرده و از طریق سایر مراکز خونی و با تقاضای اورژانسی برآورده می‌شوند.

6.       اگر تقاضای اورژانسی بیمارستان‌ها کمتر از موجودی در دست مرکز خونی باشد، پس از برآورد تقاضاها، پلاکت‌های باقی‌مانده با طول عمر یک روز، دورریز می‌شوند و هزینه‌ اتلاف بر مرکز خون تحمیل می‌کنند و پلاکت‌های با طول عمر دو و سه‌روزه، به روز بعد منتقل می‌شوند.

7.       در پایان هر دوره مرور، موقعیت موجودی مرکز خون تعیین می‌شود و اگر کمتر از s و یا برابر آن باشد، سفارش صادر می‌شود که بعد از گذشت مدت زمان تحویل، پلاکت‌های سفارش‌داده‌شده به مرکز خون می‌رسند و در غیر این صورت، سفارش انجام نمی‌شود.

تابع هدف:

تابع هدف در این مدل به دنبال حداقل کردن هزینه‌های زنجیره تأمین است که متشکل است از:

·         هزینه‌های بیمارستان‌ها:

o         هزینه‌های عملیاتی

o         هزینه‌های حمل‌ونقل

o         هزینه‌های خرید خون

o         هزینه‌های نگه‌داری

o         هزینه‌های اتلاف خون

o         هزینه‌های کمبود خون

·         هزینه‌های مرکز خون:

o         هزینه‌های عملیاتی

o         هزینه‌های حمل‌ونقل

o         هزینه‌های نگه‌داری

o         هزینه‌های اتلاف خون

o         هزینه‌های کمبود خون

محدودیت‌ها:

محدودیت‌های (2) و (3): بیان می‌کند تعداد واحدهای خونی که در یک دوره معین به بیمارستان می‌رسند، برابر است با تعداد واحدهای خونی است که قبلاً سفارش داده شده‌اند و اکنون بعد از سپری شدن مدت زمان تحویل (lead time)، به بیمارستان می‌رسند.

محدودیت‌های (4-6): تعادل موجودی-تقاضا در بیمارستان‌ها را نشان می‌دهند در صورتی که سیاست اعمال‌شده در بیمارستان‌ها FIFO باشد.

محدودیت (7): بیان می‌کند که بعد از ارضای تقاضاها در یک روز، پلاکت‌هایی که طول عمر آن‌ها یک روز است، دورریز می‌شوند.

محدودیت (8): موقعیت موجودی بیمارستان‌ها را محاسبه می‌کند.

محدودیت‌های (9-13): این محدودیت‌ها تضمین می‌کنند تحت اعمال سیاست (s,S) که اگر موقعیت موجودی بیشتر از نقطه سفارش مجدد یا برابر آن باشد، سفارشی صادر نمی‌شود و در غیر این صورت، سفارش به مقداری صادر می‌شود که موقعیت موجودی به S برسد.   

محدودیت (14): بیان می‌کند که سطح موجودی S باید بزرگتر از نقطه سفارش‌دهی (s) مجدد باشد.

محدودیت (15) و (16): به‌روزرسانی موجودی در بیمارستان‌ها را نشان می‌دهد.

محدودیت (17): میزان کمبود خون در بیمارستان‌ها را در هر روز محاسبه می‌کند.

محدودیت (18): نشان‌دهنده سطح موجودی اولیه در هر بیمارستان است.  

محدودیت (19): بیان می‌کند که پلاکت فقط در دوره مرور موجودی می‌تواند سفارش داده‌شود.

محدودیت‌های (20) و (21): تعداد واحدهای پلاکت موجود در ابتدای هر روز را در مرکز خون و تحت هر سناریو محاسبه می‌کند.

محدودیت‌های (22-24): بیان می‌کنند که اگر مدت زمان تحویل برای بیمارستانی یک روز باشد، فقط پلاکت‌های با طول عمر دو و سه‌روزه می‌توانند به این بیمارستان‌ها منتقل شوند و هم‌چنین، اگر مدت زمان تحویل برای بیمارستانی دو روز باشد، فقط پلاکت‌های با طول عمر سه‌روزه می‌توانند به این بیمارستان‌ها منتقل شوند و در صورتی که مدت زمان تحویل برای بیمارستانی ناچیز باشد، پلاکت با هر طول عمری می‌تواند به این بیمارستان‌ها فرستاده‌شود.

محدودیت (25): میزان کمبودهایی را که در مرکز خون و به دلیل تقاضاهای معمولی رخ می‌دهد، محاسبه می‌کند.

محدودیت (26): بیان می‌کند که تعداد واحدهای پلاکت سه‌روزه که از مرکز خون به یک بیمارستان فرستاده می‌شود، برابر است با مجموع تعداد واحدهای پلاکت سه روزه که از موجودی در دسترس در مرکز خونی که به بیمارستان فرستاده می‌شود و میزان واحدهای کمبود که مرکز خون به دلیل تقاضاهای معمولی متحمل می‌شود.

محدودیت (27-29): تعادل موجودی-تقاضا در بیمارستان‌ها نشان می‌دهند، هنگامی که تقاضای اورژانسی وجود داشته‌باشد.

محدودیت (30): کل کمبودهایی را که در مرکز خون رخ می‌دهد، محاسبه می‌کند.

محدودیت‌ (31): موقعیت موجودی را در مرکز خون نشان می‌دهد.

محدودیت‌های (32-37): مشابه محدودیت‌های (9-14)  مقدار سفارش‌ها را در مرکز خون محاسبه می‌کنند.

محدودیت (38): تعداد واحدهای پلاکت فاسدشده را در انتهای هر روز در مرکز خون نشان می‌دهد.

محدودیت (39-40): سطح موجودی را در انتهای هر روز در مرکز خون به‌روز می‌کنند.

محدودیت (41): تعداد واحدهای کمبود در مرکز خون را در هر روز و تحت هر سناریو محاسبه می‌کند که ناشی از تقاضاهای معمولی و تقاضاهای اورژانسی برآورده نشده در بیمارستان‌ها هستند.

محدودیت (42): نشان‌دهنده سطح موجودی اولیه در هر مرکز خون تحت هر سناریو است. 

محدودیت‌های (43-45): انواع متغیرها را تعیین می‌کند.

روش حل:

الگوریتم ژنتیک، یک الگوریتم فراابتکاری است که بر پایه فرآیند‌ انتخاب طبیعی و فرآیند تکامل شکل گرفته‌است. هر جواب کاندید در این الگوریتم که تحت عنوان کروموزوم شناخته می‌شود، از رشته‌ای از ژن‌ها تشکیل شده‌است که ساختار این ژن‌ها در هر کروموزوم بسته به هر مسئله متفاوت است. هر کروموزوم در طی نسل‌های مختلف با بهره‌گیری از عملگرهای تقاطع و جهش تکامل می‌یابد و منجر به بهبود تدریجی تابع هدف می‌شود. در دهه‌های اخیر، از الگوریتم‌ ژنتیک به عنوان یکی از الگوریتم‌های فراابتکاری پرکاربرد در حل مسائل مدیریت موجودی شناخته شده‌است.

در این مقاله، نوع جدیدی از الگوریتم ژنتیک توسعه داده شده‌است که با توجه به رویکردهایی که در انتخاب کروموزوم‌های نسل‌های بعدی به‌کار گرفته شده‌است، انتظار می‌رود که دارای سرعت همگرایی بیشتری داشته‌باشد. جواب‌های حاصل از این الگوریتم، با سایر الگوریتم‌های ژنتیک توسعه‌داده‌شده موجود در ادبیات، مقایسه شده‌اند و هم‌چنین، در این مقاله برای تنظیم پارامترها از طرح‌های عاملی کامل (full factorial design) بهره گرفته شده‌است.

گام‌های الگوریتم پیشنهادی در این مقاله که الگوریتم ژنتیک تصادفی اصلاح‌شده (modified stochastic genetic algorithm یا به طور خلاصه MSGA) نامیده شده‌است، به صورت زیر است:

شکل4. شبه‌کد الگوریتم MSGA

در این الگوریتم، ابتدا جمعیت اولیه برای مسئله موجودی زنجیره تأمین خون تولید می‌شود و در گام بعدی، مقدار تابع شایستگی برای این جواب اولیه محاسبه می‌شود. سپس، عملگرهای تقاطع و جهش، مطابق توضیحات موجود در شکل 4، وارد عمل می‌شوند. در الگوریتم‌های ژنتیک مرسوم، تنها فرزندان به عنوان نتایج حاصل از عملگرهای تقاطع و جهش به نسل بعدی منتقل می‌شوند و والدین، حتی اگر از شایستگی بسیار بالایی نیز برخوردار باشند، به نسل بعدی منتقل نمی‌شوند و در همین نسل باقی می‌مانند که این موضوع، ممکن است منجر به ایجاد جواب بهینه محلی شده و یا باعث کند شدن همگرایی الگوریتم شود. به‌همین دلیل، در الگوریتم MSGA انتخاب کروموزوم‌ها برای انتقال به نسل بعدی به نحوی دیگر انجام می‌شود و انتخاب کروموزم منتقل‌شده به نسل بعد، از میان مجموعه فرزندان و والدین با توجه به شایستگی آن‌ها انجام می‌شود.

نتایج:

در این مقاله، برای بررسی کارایی مدل و الگوریتم پیشنهادی از یک مطالعه موردی استفاده شده‌است. ابتدا، عملکرد الگوریتم MSGA با مدل برنامه‌ریزی عدد صحیح احتمالی برای مسائلی با ابعاد کوچک بررسی شده‌است. نتایج نشان‌دهنده آن است که هزینه حاصل از الگوریتم پیشنهادی در مقاسه با مدل احتمالی بیشتر است. از دلایل این هزینه زیاد، می‌توان به وجود سطح بالای کمبود در مراکز خونی در حل با الگوریتم اشاره کرد و این در حالی است که سطح کمبود در مدل احتمالی بسیار کمتر است. با این وجود، مدت حل مسئله با الگوریتم MSGA در حدود 8 دقیقه است و این در حالیست که دستیابی به جواب بهینه در مدل احتمالی حدود یک ساعت طول کشیده‌است.

برای مسائل با ابعاد بزرگ، الگوریتم MSGA با الگوریتم پایه ژنتیک احتمالی(base SGA) و الگوریتم شبیه‌سازی تبرید (SA) مقایسه شده‌است. نتایج گویای آن است که مقدار تابع هدف (هزینه کل) الگوریتم MSGA در مقایسه با مقدار تابع هدف‌های الگوریتم‌های SGA و SA بهتر است. با توجه به این که خطای حل نسبتاً کم است، با این وجود اختلاف بین هزینه‌ها از لحاظ آماری قابل‌توجه است و نتایج تست ANOVA نیز گواهی بر این موضوع است. به علاوه، سرعت همگرایی SA در مقایسه با دو الگوریتم دیگر بسیار کمتر است. از لحاظ تعداد واحدهای خریداری شده، بیمارستان‌ها و مراکز خونی در حل با الگوریتم MSGA و SA، واحدهای بیشتری را در مقایسه با SGA خریداری می‌کنند که همین عامل باعث اتلاف واخدهای خونی بیشتر دربیمارستان‌ها و مراکز خونی می‌شود. از طرف دیگر، تعداد خرید تعداد واحدهای خونی کمتر در الگوریتم SGA باعث افزایش کمبود در بیمارستان‌ها و مراکز خونی می‌شود. با توجه به نتایج آزمون ANOVA تک عاملی که نشان‌دهنده نوسانات زیاد در مقدار تابع هدف در روش SA است و با توجه به این که سرعت همگرایی آن نیز، نسبتاً کم است، بنابراین SA در مقایسه با دو الگوریتم دیگر عملکرد قابل قبولی از خود نشان نمی‌دهد. هم‌چنین برای مقایسه بیشتر آزمون Tukey نیز انجام شده‌است که نتایج آن نشان می‌دهد این سه الگوریتم از لحاظ آماری دارای تفاوت معنی‌داری هستند.

هم‌چنین، تحلیل حساسیت روی پارامترهای مهم مدل مانند هزینه‌ها، مقدار تقاضاها و تعداد بیمارستان‌های موجود در شبکه انجام‌ شده‌است که حاوی رهنمودهای مدیریتی مهمی برای تصمیم‌گیرندگان است. نتایج بیانگر آن است که مدل پیشنهادی، دارای عملکردی استوار در مقابل تعداد بیمارستان‌ها است و از این رو می‌توان از این مدل برای مدیریت موجودی محیط‌های بزرگ مانند مناطق روستایی و شهری استفاده کرد. به‌علاوه، در مواردی که بیمارستان‌ها با نوسانات تقاضای زیادی مواجه هستند، پیشنهاد می‌شود که از الگوریتم MSGA برای حل مدل استفاده کرد. هم‌چنین در مواردی که هزینه خرید خون دارای اختلاف زیادی با هزینه‌های به‌کاررفته در این مقاله باشد، استفاده از الگوریتم MSGA توصیه می‌شود.