طراحی یک شبکه استوار و پویا برای زنجیره تامین خون اضطراری با خطر بروز اختلالات (مقاله چهارم)

چکیده

در این مقاله یک مدل استوار و دارای قابلیت اطمینان برای یک مساله طراحی شبکه اضطراری پویا ارائه شده است. برای کنترل در برابر خطر ایجاد اختلال از تکنیک  p-criterion استفاده شده است. به ‌علاوه با استفاده از دو مثال، عملکرد مدل تحت هر نوع ریسک را به طور جداگانه بررسی کرده است.. نتایج نشان می دهد که عملکرد مدل کاملاً رضایت بخش است .

کلید واژه:  طراحی شبکه پویا، زنجیره تامین خون، بحران، قابلیت اطمینان، بهینه سازی استوار، اختلال در تسهیلات

 مقدمه

امروزه یکی از مهمترین مشکلات در صنعت، مشکل طراحی شبکه عرضه است. تنوع صنایع و الزامات آنها برای زنجیره تأمین به تعداد زیادی مدل، نیاز دارد. به عنوان مثال، در برخی موارد، تحویل سریع محصول آن از اهمیت حیاتی برخوردار است، از جمله مشکل تهیه و تحویل تجهیزات نظامی و یا اعزام نیرو به منطقه. در برخی موارد دیگر، تحویل ایمن برخی از محصولات حیاتی با حداقل خسارت، مهمترین ویژگی طراحی زنجیره تأمین مانند تحویل بسته مواد غذایی و کالاهای اساسی توسط سازمان ملل متحد به مناطق جنگ زده، مناطق خشکسال یا تخلیه افراد از این مناطق است. یکی از این مشکلات، طراحی شبکه زنجیره تأمین برای تهیه خون است. می توان ادعا کرد که در این موارد، تأخیر در خون رسانی به ضرر انسان منجر می شود که این امر بر اهمیت تحویل به موقع این محصول ارزشمند، تأکید دارد. به دلیل احتمال زیاد صدمات و این واقعیت که هرگونه کمبود خون ممکن است منجر به مرگ تعداد قابل توجهی از افراد شود، وضعیت در مقابل یک بحران بدتر می شود. بحران یا طبیعی است (زلزله ، سونامی ، سیل ، فوران آتشفشانی و غیره) یا ساخته شده توسط انسان (حملات تروریستی، نشت گاز، بلایای هسته ای و غیره).

رویکردهای اولیه برای طراحی شبکه زنجیره تأمین این است که تمام پارامترهای مدل، مانند تقاضای خون و برخی از هزینه ها را در طول افق برنامه ریزی مسئله، ثابت و تعیین کننده در نظر میگیرند. در حالی که این فرض باعث می شود روند یافتن جواب مناسب بطور قابل توجهی آسان تر شود. اما در واقعیت، پیش بینی دقیق مقادیر این پارامترها در مواجهه با فاجعه تقریبا غیرممکن است زیرا هیچ راهی برای تخمین شدت فاجعه وجود ندارد. علاوه بر این، واضح است که هر اشتباهی در برآورد این مقادیر می تواند فاجعه بار باشد. به همین دلیل برای یافتن جواب مناسب برای موقعیت های مختلف، از مفهوم عدم  قطعیت پارامتر و بهینه سازی استوار را در مساله طراحی شبکه زنجیره تامین خون در صورت بروز فاجعه استفاده میشود.

از طرف دیگر، بررسی ادبیات نشان می دهد که بیشتر مدل های ارائه شده تاکنون فرض می کنند که عناصر شبکه خون رسانی، یعنی تسهیلات جمع آوری خون و مراکز ذخیره سازی خون، تحت تأثیر فاجعه قرار نخواهند گرفت. با در نظر گرفتن این فرض، جواب به دست آمده از احتمال اختلال در تسهیلات و مرکز محافظت نمی کند (به خصوص در صورت بروز فاجعه در مقیاس بزرگ مانند سونامی). در نتیجه، بهتر است که احتمال اختلال در تسهیلات خون و مرکز در مدل در نظر گرفته شود.

در این مقاله، یک مدل استوار و دارای قابلیت اطمینان برای جمع آوری خون از گروه های اهدا کننده، مکان یابی بهینه برای  تسهیلات جمع آوری خون دائمی و موقت و اختصاص گروه های اهدا کننده به مراکز جمع آوری خون و همچنین تسهیلات جمع آوری خون در مراکز ذخیره خون ارائه شده است. عدم قطعیت در مورد مقادیر پارامترها با استفاده از روش بهینه سازی استوار در مساله در نظر گرفته شده است. در این مقاله سعی شده است یک برنامه استراتژیک برای فرایند برنامه ریزی قبل از فاجعه مشخص شود، تا بتواند به برنامه ریزی برای بروز فاجعه کمک کند.

نوآوری:

هدف از این پژهش ارائه الگویی واقع بینانه تر از تحقیقات انجام شده در زمینه طراحی شبکه زنجیره تامین خون در مواجهه با بحران است. این مدل با عدم اطمینان نسبت به مقادیر پارامتر و وضعیت تسهیلات پس از فاجعه سازگاری بیشتری خواهد داشت. سهم عمده  این پژوهش را می توان به شرح زیر خلاصه کرد:

·            در نظر گرفتن،  قابلیت اطمینان و استواری برای غلبه بر اختلالات و عدم قطعیت

·            در نظر گرفتن ماهیت پویای تقاضای خون در مدل پیشنهادی

·            در نظر گرفتن خطر ایجاد اختلال در مراکز خونی و تسهیلات جمع آوری دائمی خون در فاجعه

·            ارائه رویکرد گسسته و پیوسته ترکیبی در مورد اختلالات و عدم اطمینان

·             ایجاد یک مدل قابل اطمینان با استفاده از معیار p-robust برای کاهش اثرات اختلال در سیستم

·            حل مدل با استفادع از الگوریتم آزاد سازی لاگرانژ

بهینه سازی استوار:

رویکرد مورد استفاده در این مقاله، یک رویکرد بهینه سازی خطی بر اساس مجموعه های عدم قطعیت چند بعدی می باشد. که بر خلاف روش های استوار قبلی، این رویکرد به پیچیدگی مسئله مورد بررسی اضافه نمی کند. این روش بر اساس این فرض استوار است که هر پارامتری دربررسی عدم قطعیت موجب ایجاد جواب های متفاوت میشوند. مدل در فرمول (1) معرفی شده است:

 ماتریس A که دارای عدم قطعیت میباشد را به صورت زیر در نظر میگیریم:

لازم به ذکر است که در صورتی ماتریس C’ هم دارای عدم قطعیت باشد، باید محدودیت Z - C’x<=0  را به مدل اضافه کرده و سپس تابع هدف را به صورت Max Z بازنویسی کرد.

با فرض اینکه تنها عناصر ماتریس A  دارای عدم قطعیت هستند، فرمول (1) را می توان همانطور که در مدل (4) نشان داده شده است بازنویسی کرد.

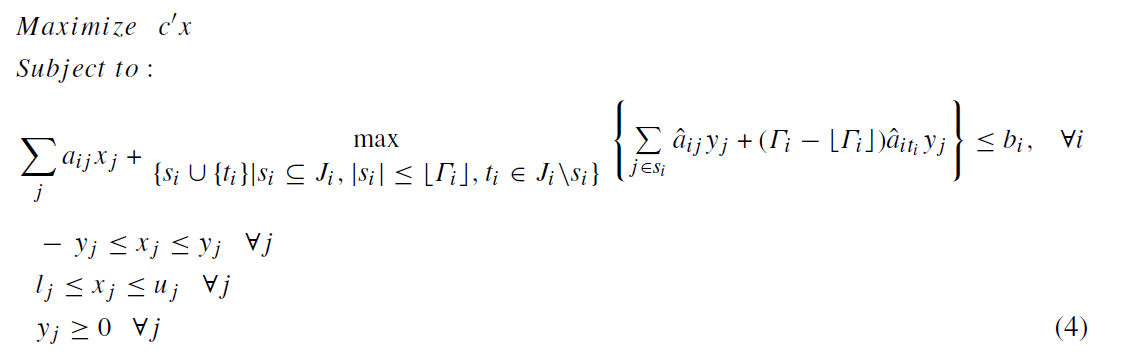
نمادهای مورد استفاده در مدل (4) به شرح زیر است:

i  : سطرهای ماتریس A

 J_i : مجموعه پارامترهای دارای عدم قطعیت در سطر  Jام ماتریس A

˜ai j  : پارمتر دارای عدم قطعیت که هر محدوده از دامنه [￣ai j − ˆai j , ￣ai j + ˆai j ] را به خود اختصاص دهد که  ￣ai j   مقدار اسمی و  ˆai j  حداکثر فاصله آن از مقدار اسمی است.

ηi j : متغیر تصادفی که بازه تغییرات آن بین بین به 1 − تا 1 است و توسط فرمول زیر  محاسبه می شود:

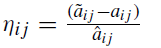
Γi:  ضریب درجه محافظه کاری (استواری)، که نشان می دهد سطح ریسک گریزی برای هر سطر i که لزوماً عدد صحیح نیست و ممکن است هر مقداری را در دامنه [0,|Ji |] به خود اختصاص دهد.

مجموعه عناصر دارای عدم قطعیت  از دو زیر مجموعه تشکیل شده است:

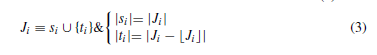
اولین محدودیت  مدل 4 را به صورت زیر بازنویسی کرده:

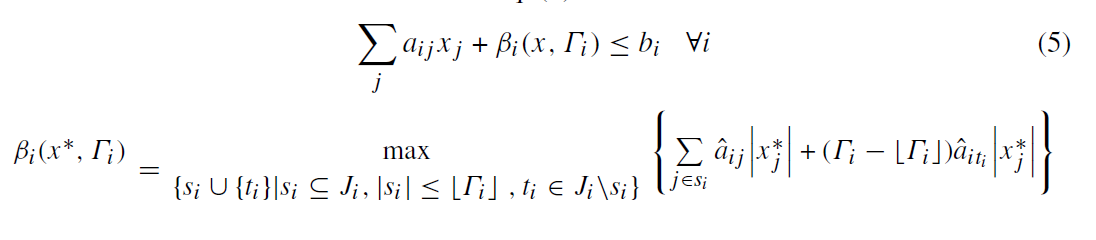
 فرض میشود  X∗  جواب بهینه میباشد پس تابع محافظتی به صورت زیر بازنویسی میشود:

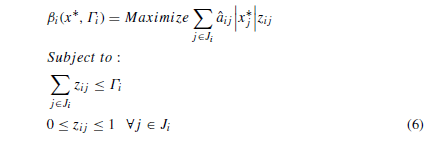
فرم دوگان مساله به صورت زیر نوشته میشود:

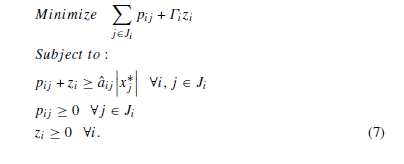
با وارد کردن مدل (8) در مدل (4) و با توجه به فرمول (5) و (6) در بالا ، می توان مدل خطی نهایی را به شرح زیر نوشت:

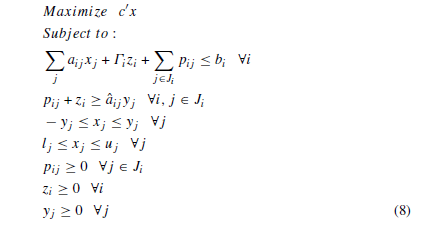
با توجه به ساختار مدل پیشنهادی، می توان مسئله خطی را حل کرد و در شرایط عدم قطعیت کامل بهینه سازی استوار، به جواب بهنیه رسیده است.   Γi ضریب درجه محافظه کاری، باعث ایجاد یک موازنه بین نقض محدودیت و تأثیرگذاری بر تابع هدف اصلی مسئله میشود که به عنوان هزینه استوار شناخته می شود.

اگر در این رویکرد  x ^∗  جواب بهینه استوار مدل باشد. احتمال نقض محدودیت  iام  را میتوان با فرمول زیر محاسبه کرد (φ (θ) تابع توزیع تجمعی یک متغیر تصادفی عادی استاندارد است) :

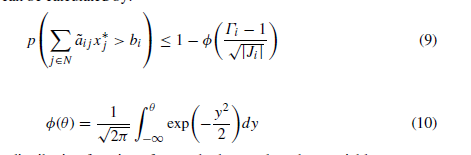
همزاد قابلیت اطمینان

در این مقاله رویکرد Snyder and daskin 2006 برای نشان دادن مفهوم قابلیت اطمینان، مورد استفاده قرار گرفته است. با توجه به این رویکرد، مدل پیشنهادی سناریوهای اختلال چندگانه برای تسهیلات جمع آوری خون و مراکز خون، با هدف یافتن جوابی که کمترین تأثیر را بر احتمال اختلال در تسهیلات و مرکز داشته باشد، در نظر گرفته است.

مدل استوار و دارای قابلیت اطمینان

یک مدل استوار و دارای قابلیت اطمینان برای طراحی زنجیره تامین خون که در برابر بحران قابل تاب آوری باشد ارائه شده است. زنجیره تأمین شامل اهداکنندگان خون، تسهیلات خون و مراکز خونی است. مراکز خون عملیات مربوط به انتقال خون مانند جمع آوری، آزمایش، پالایش، ذخیره و توزیع را انجام می دهند. تسهیلات خون دو نوع میباشند: (1) تسهیلات دائمی با محل ثابت در همه دوره ها و ظرفیت زیاد و (2) تسهیلات موقت خون با ظرفیت کمتر و امکان قرارگیری در موقعیت های مختلف (مانند اتوبوس خون).

در این مسئله، هدف تعیین محل تسهیلات جمع آوری دائمی و موقت خون ، تخصیص گروه های اهداکننده به این تسهیلات و محاسبه میزان خون جمع آوری شده از گروه های اهدا کننده و ارسال به مراکز خون و هزینه کل تحمیل شده در مورد یک فاجعه به روشی مطمئن و استوار را به حداقل برسانند. در بسیاری از موارد در دنیای واقعی، کمبود خون به دلایل مختلف از جمله پایین بودن میزان اهدای خون، آلودگی خون و تسهیلات جمع آوری خون یا اختلال در مرکز خون میباشند. با توجه به اینکه کمبود خون مستقیماً می تواند منجر به از بین رفتن انسان شود، در مدل پیشنهادی یک مجازات برای تقاضای خون رضایت بخش در نظر گرفته می شود و ارزش آن در طول اجرای مدل کنترل می شود. برای طراحی چنین شبکه ای، تابع  هدف مسئله شامل به حداقل رساندن هزینه ها در زمان وقوع یک فاجعه است.

برای واقعی تر شدن مسئله، پارامترهای هزینه خون، حمل و نقل تسهیلات و هزینه عملیاتی غیر قطعی در نظر گرفته شده است. علاوه بر این، تقاضای خون نیز در معرض عدم قطعیت است.  علاوه بر عدم قطعیت در مورد پارامترهای مدل، یکی دیگر از عوامل، احتمال خطر مختل شدن تسهیلات در هنگام فاجعه است. در نظر گرفتن سناریوهای مختلف اختلال مربوط به تسهیلات یا مرکز، به یافتن جواب مناسب تر برای یک وضعیت در دنیای واقعی که به عنوان "قابلیت تاب آوری مدل" شناخته می شود، کمک می کند.

همانطور که گفته شد در صورت بروز بحران، مراکز خدماتی و همچنین امکانات در معرض اختلال هستند. در صورت اختلال در یک مرکز خون از از تقاضای آن صرف نظر نخواهد شد و به مراکز باقی مانده اختصاص می یابد و در نتیجه باعث تغییر تقاضای خون اولیه آن ها شود.

که این موضوع  با استفاده از فرمول (11) در مسئله نشان داده  شده است:

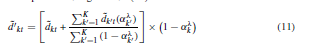
مدل استوار و دارای قابلیت اطمینان پیشنهادی (RRM) :

تابع هدف (12): هزینه کل را که شامل هزینه های احداث تسهیلات جمع آوری خون، حمل و نقل، هزینه های عملیاتی و نگهداری خون و مجازات های کمبود است، به حداقل می رساند. بخش اول درتابع هدف، هزینه احداث تسهیلات جمع آوری دائمی خون را نشان می دهد. در بخش دوم، کل هزینه نگهداری خون تحت سناریو صفر محاسبه می شود که در آن هیچ یک از تسهیلات مختل نیست. بخش سوم، هزینه کل تقاضای ناراضی را تحت عنوان سناریو صفر نشان می دهد. در بخش  چهارم کل هزینه جابجایی تسهیلات جمع آوری خون موقت بین مکان های منتخب  تحت سناریو صفر محاسبه می شود. کل هزینه انتقال خون اهدا شده از مراکز جمع آوری خون به مراکز خونی تحت سناریو صفر در بخش پنجم ارائه می شود. کل هزینه عملیاتی جمع آوری خون در بخش ششم تحت سناریو صفر محاسبه می شود. در مدل ارائه شده فقط پارامتر های اسمی نشان داده شده است پس به منظور نشان دادن عدم قطعیت این مقادیر در مدل، شش بخش بعدی از طریق روشی که توسط استواری که شرح داده شده است به تابع هدف اضافه می شود.

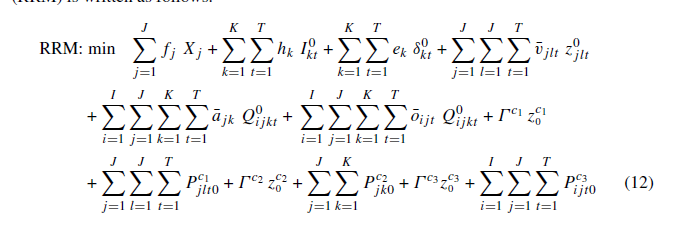
محدودیت (13)، که به منظور قابلیت اطمینان به مدل اضافه شده است، مانع از این میشود که جواب، هزینه ای بیش تر از (1+p)%  از جواب بهینه F^∗ _λ داشته باشد.

برای تعیین مقدار بهینه، تابع هدف F^∗ _λ ، مدل زیر (29) باید برای هر سناریو λ حل شود.

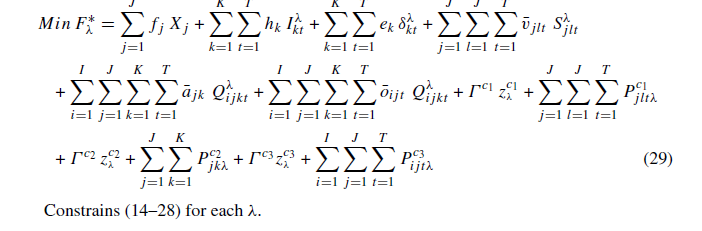
محدودیت ها (14) - (18) : با توجه به روش بهینه سازی استوار که شرح داده شده است به مدل اضافه می شود.

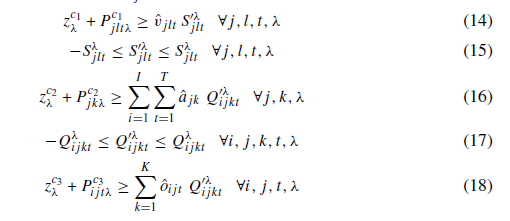
محدودیت (19):  بیانگر ارتباط بین سطح موجودی، تقاضا و کمبود خون در هر مرکز برای هر دوره است.

محدودیت (20):  اختصاص تسهیلات جمع آوری موقت خون را در مناطقی که تسهیلات دائمی وجود ندارد و یا  تسهیلات آن مناطق مختل می شود، را تضمین میکند.

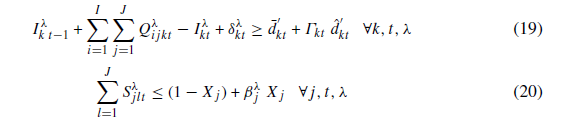
محدودیت (21): فقط مکان هایی که در دوره قبلی دارای تسهیلات جمع آوری موقت خون هستند می توانند تسهیلات جمع آوری موقت خون خود را به مناطق دیگر ارسال کنند.

 محدودیت (22): محدوده پوشش هنگام اختصاص اهداکنندگان به مکان ها را تضمین می کند.

محدودیت (23): تضمین می کند که از ظرفیت جمع آوری خون در هر مرکز تجاوز نمی شود.

محدودیت (24): خون فقط می تواند از گروه اهدا کننده i در محل j دریافت شود و به مرکز  k ارسال شود  درصورتی که گروه اهدا کننده در مکان j قرار داشته باشد  مشروط بر اینکه هیچ  تسهیل یا مرکزی مختل نشود.

محدودیت (25):  تضمین می کند که اهدا کنندگان فقط می توانند به تسهیلات موقت که به آن مکان اختصاص یافته اند یا مراکز جمع آوری خون دائمی که مجهز شده اند و مختل نشده اند، اختصاص یابد.

محدودیت (26): تضمین میکند که مقدار خون جمع آوری شده از ظرفیت تسهیلات دائمی یا موقت جمع آوری خون تجاوز نکند.

 محدودیت (27):  محدودیت ظرفیت خون اهدا کنندگان را اعمال میکند.

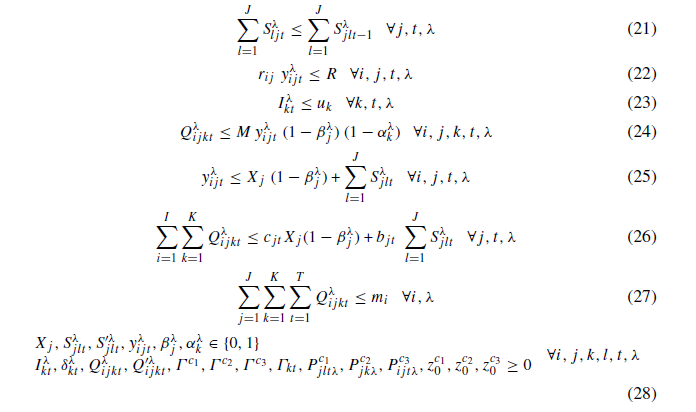
روش حل

در این بخش، یک الگوریتم مبتنی بر آزاد سازی لاگرانژ برای یافتن یک جواب تقریبا بهینه برای مسئله در اندازه های بزرگ تهیه شده است. آزاد سازی لاگرانژ یک رویکرد راه حل استوار با کاربردهای بارز در حل مسائل بهینه سازی زنجیره تأمین است. که می تواند حد های بالا و پایین را با یک مقدار هدف مطلوب ایجاد کند. در این مقاله روش آزاد سازی لاگرانژ توسعه داده شده است که هدف آن کاهش فاصله بین حد بالا و پایینن به صورت تکرار در سه مرحله است. اول، یک حد پایین برای  جواب بهینه پیدا می شود، دوم یک حد بالایی برای جواب بهینه بدست می آید، و در نهایت در صورت عدم دسترسی کافی، مرزهای بالا و پایین در هر تکرار به روز می شوند. این روند تکراری تا رسیدن به مرزهای پایین و بالا با توجه به نزدیک بودن ادامه می یابد.

حد پایین:

الگوریتم تکرار پذیر لاگرانژ، برای بدست آوردن مرزهای پایین استفاده شده است.  مدل مسئله LGRP برای آزاد سازی مجموعه ای از محدودیت ها (22) ، (24) و (25)به شکل زیر است:

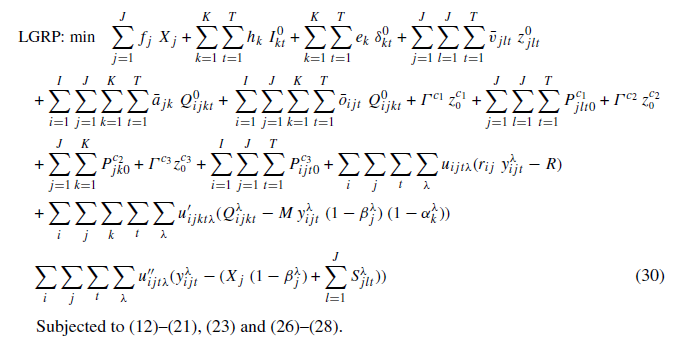
حد بالا:

در هر تکرار از روش آزاد سازی لاگرانژ  یک حد پایین با حل LGRP تعیین می شود. به دلیل رفع محدودیت (22) ، (24) و (25)، هیچ تضمینی برای اختصاص گروه اهدا کننده به تسهیلات مجموعه در محدوده پوشش داده شده وجود ندارد. در این حالت، جواب LGRP یک جواب شدنی نیست. برای تولید یک جواب شدنی، مجموعه متغیرهای تصمیم Xj برابر مقادیر بهینه بدست آمده از حل LGRP هستند و سپس مدل RRM را حل می کنند. در این حالت، مکان تسهیلات دائمی در حین حل RRM مشخص شده است، بنابراین گروه های اهدا کننده که در محدوده پوشش تسهیلات دائمی قرار ندارند، به تسهیلات موقتی اختصاص می دهند. در نتیجه یک حد بالایی برای RRM فراهم می شود.

به روز رسانی:

پس از اجرای الگوریتم، از مقادیر بهینه حاصل از حل مسئله LGRP برای به روزرسانی به شرح زیر استفاده می شود:

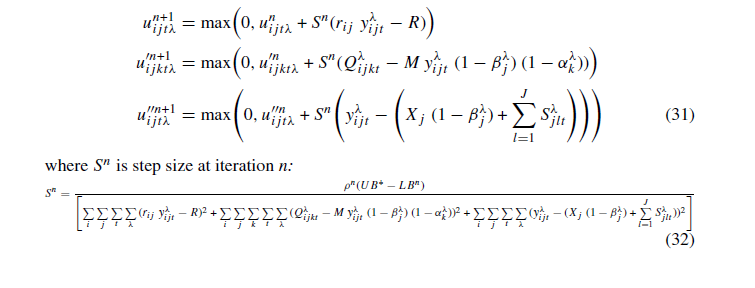
در فرمول فوق، ρⁿ ثابت در تکرار t است و در ابتدا روی 2 تنظیم می شود. اگر حد پایین از 30 تکرار متوالی بهبود نیابد، مقدار pⁿ  به 2 تقسیم می شود. همچنین UB ^*بهترین حد بالایی است که از طریق تمام تکرارهای گذشته تشخیص داده می شود و LBⁿ بیانگر حد پایین به دست آمده از تکرار قبلی است. الگوریتم با دو شرط زیر خاتمه می یابد:

 نتیجه گیری

در این مقاله، مفاهیم استواری و قابلیت اطمینان در مسئله طراحی زنجیره تامین خون در بحران نشان داده شده است. زنجیره تأمین شامل گروه های اهداکننده، تسهیلات جمع آوری موقت و دائمی خون و مراکز خونی است که خون اهدا شده در آن ذخیره می شود. در حالی که تحقیقات زیادی در مورد طراحی زنجیره تامین خون انجام شده است، خطر ایجاد اختلال کمتر مورد بررسی قرار گرفته است.

مطالعات انجام شده تاکنون رویکردی استوار و دارای قابلیت اطمینان در زنجیره تأمین خون پویا در فاجعه ارائه نداده است. هدف از مدل پویا پیشنهادی، محافظت از جواب در برابر خطر بروز اختلالات و خطر عدم اطمینان، به طور هم زمان است. این می تواند به عنوان ابزاری برای به حداقل رساندن کل تلفات انسانی و همچنین اختلالات مرکز و تسهیلات در دنیای واقعی مورد استفاده قرار گیرد. علاوه بر این، تجزیه و تحلیل حساسیت، قابلیت اطمینان و استواری  مدل پیشنهادی را تأیید می کند. بنابراین به مدیران و تصمیم گیران کمک می کند تا در هر سطح از درجه محافظه کاری خود، زنجیره تامین خون مطمئن تر و استوار تر را طراحی کنند. رویکرد راه حل مبتنی بر رویکرد آزاد سازی لاگرانژ ارائه شده است و یک مطالعه محاسباتی برای نشان دادن کارآیی و اثربخشی این رویکرد انجام شده است. در مرحله بعد، عملکرد مدل در مسئله در مقیاس بزرگ با رویکرد راه حل پیشنهادی مورد بررسی قرار گرفته و نتایج نشان می دهد که عملکرد مدل کاملاً رضایت بخش است.