
وبلاگ همافزایی دانشجویان دکتر حسینی مطلق- motlagh@iust.ac.ir
دانشکده مهندسی صنایع- دانشگاه علم و صنعت ایران
وبلاگ همافزایی دانشجویان دکتر حسینی مطلق- motlagh@iust.ac.ir
دانشکده مهندسی صنایع- دانشگاه علم و صنعت ایرانپیوندها
دستهها
جدیدترین یادداشتها
همه- ارزیابی توزیع کمبود در سیستمهای موجودی دورهای با تقاضاهای درونزای تصادفی و زمانهای تحویل (مقاله بیست و نهم)
- طراحی استراتژیهای کنترل برای کمک به جلوگیری از گسترش پاندمی COVID-19
- تعامل استراتژیک بین معرفی برند فروشگاه و معرفی کانال آنلاین مستقیم (مقاله بیست و نهم)
- کنترل موجودی و قیمت گذاری همزمان در یک سیستم موجودی-خدمات (مقاله بیست و هشتم)
- مدل بازی دیفرانسیلی برای استراتژیهای کاهش انتشار و طراحی قرارداد در یک زنجیره تأمین دو کاناله (مقاله بیست و هشتم)
- اثر شلاقی و تحلیل پیچیدگی در یک زنجیره تأمین چند کاناله با در نظر گرفتن بازی قیمت با حساسیت تخفیف (مقاله بیست و هفتم)
- ایجاد انعطافپذیری در زنجیره تأمین دارو از طریق موجودی و منبعیابی دوگانه (مقاله بیست و هفتم)
- طراحی قرارداد کاهش کربن برای یک زنجیره تأمین با مسئولیت زیست محیطی تحت اطلاعات نامتقارن (مقاله بیست و ششم)
- مدل ریاضی برای هماهنگی زنجیره تأمین دارو: فروش مجدد داروها در بازار جایگزین (مقاله بیست و ششم)
- تصمیمات زنجیره تأمین دو کاناله تحت اطلاعات نامتقارن با یک خردهفروش ریسکگریز (مقاله بیست و پنجم)
نویسندگان
- محمدرضا نعمت الهی 30
- کوثر نوروززاده 29
- پگاه باقرصفت 29
- محمدرضا قطره سامانی 28
- مینا نوری 16
- سمیرا ابراهیمی 16
- جوهری 16
- عباس جوکار 15
- سید مهدی حسینی مطلق 14
- آرزو سلطونی 13
- محمدجواد تشیعی 13
- سارا صمدپور 13
- سهیلا امیدی 11
- پرنیان فرخ نژاد 11
- محدثه سیف 10
- علیرضا جلالی 10
- میترا باقرینی 10
- شمیم همائی 10
- رزا زیرک پور 10
- مریم فرهمند 10
- نیلوفر گیلانی 10
- بهار سعیدیان 10
- مریم اویسی 10
- فیروزه عباسی سعدی 10
- مونا جزینانی 10
- سعید رحمانی 10
- زینب فرشادفر 10
- ثریا اعظمی 9
- چراغی 6
- راحله نعیمائی عالی 5
- محمددانیال فرجی 1
بایگانی
- اسفند 1400 1
- بهمن 1400 1
- دی 1400 2
- آذر 1400 4
- آبان 1400 9
- مهر 1400 12
- شهریور 1400 40
- مرداد 1400 30
- اردیبهشت 1400 3
- فروردین 1400 5
- شهریور 1399 2
- خرداد 1399 6
- اردیبهشت 1399 14
- فروردین 1399 20
- اسفند 1398 3
- بهمن 1398 5
- مهر 1398 3
- شهریور 1398 3
- مرداد 1398 28
- تیر 1398 3
- آذر 1397 1
- مهر 1397 3
- شهریور 1397 1
- تیر 1397 1
- فروردین 1397 4
- اسفند 1396 1
- آذر 1396 1
- شهریور 1396 2
- مرداد 1396 33
- تیر 1396 21
- خرداد 1396 13
- اردیبهشت 1396 29
- فروردین 1396 20
- اسفند 1395 15
- دی 1395 1
- آذر 1395 3
- آبان 1395 6
- مهر 1395 8
- شهریور 1395 5
- خرداد 1395 2
- اردیبهشت 1395 8
- فروردین 1395 6
- اسفند 1394 6
- بهمن 1394 5
- دی 1394 13
- آذر 1394 18
- آبان 1394 13
- مهر 1394 7
- شهریور 1394 3
- مرداد 1394 2
- تیر 1394 2
- خرداد 1394 6
- اردیبهشت 1394 12
- فروردین 1394 6
- اسفند 1393 7
- بهمن 1393 6
- دی 1393 10
- آذر 1393 19
تقویم
اسفند 1400| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 |
جستجو
بهینهسازی استوار (Robust Optimization) -قسمت دوم
مروری بر آنچه تا به حال گفته شد....
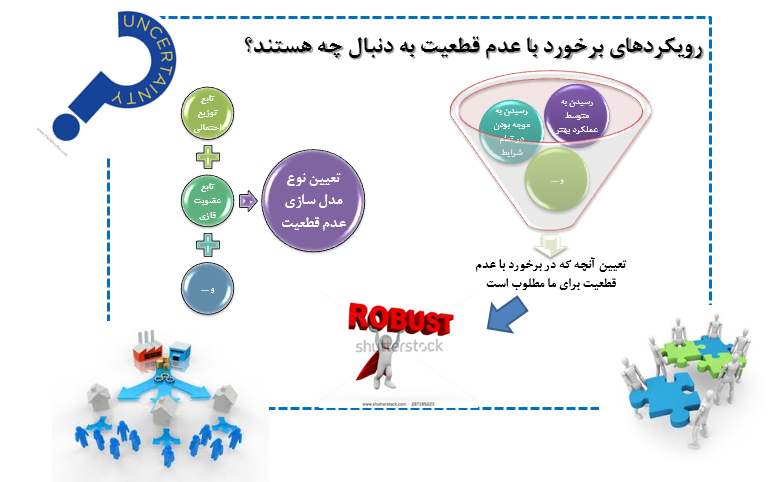
تاریخچه بهینهسازی استوار و مقالات پایه ای مهم:
به عنوان پیشتاز در این عرصه، سویستر یک روش برنامهریزی استوار بدبینانه برای برخورد با مسائل برنامهریزی خطی غیر دقیق توسعه داد. در حوزه ادبیات برنامهریزی ریاضی فازی، اولین تلاشها توسط اینگوئیچی و ساکاوا با بکارگیری رویکردهای حداقل کردن حداکثر تأسف به انجام رسید. در سال 1995، مولوی و همکاران یک روش برنامهریزی استوار منعطفتر (نسبت به حالاتی که پیشتر بیان شد) مبتنی بر مدل برنامهریزی تصادفی سناریو محور توسعه داد. این مقاله نقطه عطفی در ادبیات برنامهریزی استوار ایجاد کرد و بر مبنای آن در سالهای بعد روشهای دیگری ارائه شد. چند سال بعد بنتال و نمروفسکی و القوئی و همکاران با توسعه روش سویستر برای مسائل برنامهریزی خطی غیرقطعی با مجموعههای عدمقطعیت محدب گوناگون یک گام رو به جلوی قابل توجه در توسعه تئوری برنامهریزی استوار برداشتند.
مدل های استوار را می توان به دو شیوه دسته بندی نمود:
1- تقسیم بر اساس شرایط و ویژگی های مدل
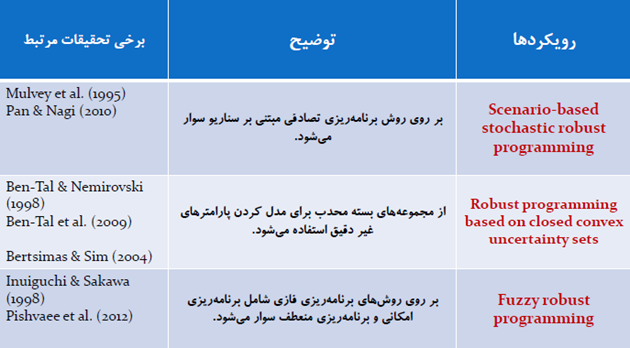
مدل های استوار محدب از میان مدل های استوار مشهروترین به حساب می آیند. شهرت این مدل ها به دلیل سادگی اثبات (بر اساس قضایای دوگان و مجموعه های محدب)، سادگی مدل و امکان تطبیق با سایر مسائل بهینه سازی است. در پست های بعدی به بررسی بیشتر این مدل ها خواهیم پرداخت. مدل های سناریو محور زمانی مناسبند که عدم قطعیت به صورت گسسته یا سناریویی رخ می دهد. امکان ترکیب مدل های بهینه سازی استوار با سایر رویکردهای مقابله با عدم قطعیت مانند رویکرد فازی نیز وجود دارد.
2- تقسیم بر اساس حساسیت کاربرد و ترجیحات گیرنده تصمیم:
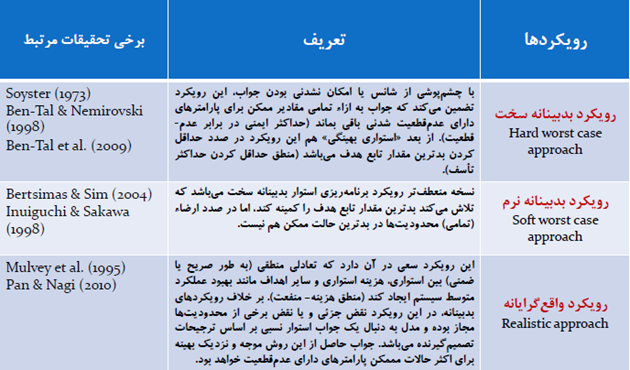
انتخاب از میان رویکردهای بالا بر اساس حساسیت مبحث مورد نظر و/یا ترجیحات گیرنده تصمیم صورت می گیرد. به عنوان مثال در حوزه بهداشت و سلامت انتخاب مدلی با رویکرد بدبینانه سخت برای برخورد با عدم قطعیت مناسب تر است، چراکه هرگونه خطا و اشتباه در این حوزه غیرقابل جبران نمی باشد و به منظور حفاظت از جان و سلامت انسان ها حاضر به پرداخت هر هزینه ای هستیم. دو رویکرد دیگر دارای محافظه کاری کمتر و در نتیجه هزینه کمتری می باشند و بر اساس توازنات هزینه ای-محافطه کاری از آنها استفاده می شود.
در پست های بعدی به بررسی جزئیات رویکردها و مدل های مختلف استوار می پردازیم.
به منظور دسترسی آسانتر به این سلسله مطالب، از این پس خوانندگان عزیز میتوانند به بخش بهینهسازی استوار در وبلاگ مراجعه نمایند.
(مونا عیسیبخش m.issabakhsh@ind.iust.ac.ir)
ممنون مونا جون از سری پست های آموزشی رباستی که میذاری...نسبتا آموزش فارسی هدفمند تو این زمینه کمه...ایشاالله مرزهای دانش تو این زمینه رو بپیمایی، رد کنی، بشکونی و خلاصه ببینم چیکار میکنی


وای دستم خورد خودم منفی دادم نظرموووو...اگه راهی داره منفیشو حذف کنید

 خنده:
خنده:
اگه میشه لطف کنید مقالات مرور ادبیاتتون رو برای من ارسال کنید خیلی ممنون میشم
با سلام
ممنون از اطلاعات مفیدی که در اختیار ما قرار دادین.
مقاله یا مثالی در مورد بهینه سازی استوار در سود خرده فروش به روش برتسیماس و سیم می خواستم ممنون میشم کمک بفرمایید.
با سلام و احترام
ممنون از مطالب مفیدتون
اگر امکانش هست مقالات مرور ادبیات برتسیماس و سیم رو در اختیار من قرار دهید
و
اینکه میتونید راهنمایی بفرمایید به چه روش میتونم محدودیتی رو به روش برتسیماس غیرقطعی کنم؟؟؟
با سلام و عرض خسته نباشید؛
خیلی ممنون بابت مطالب مفیدتون
من در رابطه با مسائل مکان یابی و بهیه سازی و کلا با مفاهیمی که در رابطه با مقالات بود مشکل داشتم. الان موضوعات را متوجه شدم. یک خواهشی هم داشتم در رابطه با حل مساله تخصیص درجه دوم (QAP) در نرم افزار متلب هم مطالبی را در اختیارمون قرار بدهید؛ممنونتون خواهم شد.
با سپاس
با سلام متاسفانه من نتونتستم به ادامه مطالبتون دسترسی پیدا کنم از طرفی وارد سایت هم نتونستم بشم وبلاگتونم همینطور با تشکر