بررسی مقالات مرتبط با زنجیره تأمین خون - بررسی مقاله هشتم

عنوان:

نوسانات اهدای خون بعد از وقوع بحران در یک زنجیره تأمین خون ناپایدار.

چکیده:

رفتار غیرقابل‌پیش‌بینی عرضه و تقاضا، مدیریت و برنامه‌ریزی زنجیره تأمین خون را به امری چالش‌برانگیز تبدیل کرده‌است. اگرچه اهدای خون در کنترل زنجیره تأمین نیست، ولی با اندیشیدن تدابیری نظیر ذخیره‌سازی خون به میزان کافی و یا با صدور درخواست فوری خون در صورت کمبود، می‌توان تا حدودی نوسانات در عرضه خون را تعدیل کرد. کمبود خون به‌خصوص در صورت وقوع بحران‌ها و بلایای طبیعی رخ می‌دهد که معمولاً با درخواست فوری اهدای خون از مردم می‌توان این کمبود را جبران کرد. با این وجود، اثرات این فراخوان عمومی در عملکرد زنجیره تأمین خون تاکنون به صورت دقیق بررسی نشده‌است. در این مقاله به این موضوع پرداخته شده‌است و به این منظور، مدلی مبتنی بر زنجیره مارکوف ارائه شده‌است که اثرات درخواست فوری خون بعد از وقوع یک بحران در زنجیره تأمین را مورد بررسی قرار داده‌است و رهنمودهای مدیریتی مهمی را برای تصمیم‌گیرندگان فراهم کرده‌است. 

 

مقدمه:

تنها منبع برای تأمین نیازهای خونی بیماران، خون‌های جمع‌آوری‌شده از اهداکنندگان است. در استرالیا، از هر سی نفر، یک نفر برای اهدای خون مراجعه می‌کند و این در حالی است که که از هر سه نفر، یک نفر در طول عمر خود به خون نیاز پیدا خواهد کرد. بنابراین، برای دستیابی به حالتی پایدار، نیاز به وجود اهداکنندگان خون مستمر است.

خون محصولی فسادپذیر است و هر کدام از فرآورده‌های خونی دارای طول عمری متفاوت می‌باشند. به‌علاوه، مدت زمانی که صرف آزمایش و پالایش خون می‌شود و اغلب حدود دو روز به طول می‌انجامد، طول عمر محصولات خونی را کاهش می‌دهد. به دلیل این ویژگی فسادپذیری، جمع‌آوری بیش از حد خون در بعضی دوره‌ها نمی‌تواند به طور مؤثر تضمین‌‌کننده تعادل در عرضه و تقاضای دوره‌های آتی در صورت وقوع افزایش ناگهانی تقاضا و یا کاهش عرضه باشد. اغلب، در شرایط بحرانی عرضه‌ی خون به طور قابل توجهی افزایش می‌یابد که در این شرایط ممکن است حجم خون‌های جمع‌آوری‌شده بسیار بیشتر از میزان خون موردنیاز باشد و این عامل ممکن است منجر به اتلاف حجم زیادی از خون‌های اهدایی گردد.

در برنامه‌ریزی زنجیره تأمین  خون باید به این نکته توجه کرد که هم جمعیت اهداکنندگان و هم تعداد دفعات اهدای خون توسط هر اهداکننده متغیر و محدود هستند. در بسیاری از کشورها جمعیت اهداکنندگان خون اندک است. به‌علاوه، هر اهداکننده پس از اهدای خون برای مدت زمان معینی از اهدا مجدد خون منع می‌شود. استمرار در اهدای خون نیز عامل مهمی است و بعضی از اهداکنندگان به طور مستمر، خون اهدا می‌کنند و بعضی کمتر و برخی نیز در طول عمر خود، کمتر از پنج بار، به اهدای خون اقدام می‌کنند. اگر سطح موجودی خون در مراکز خون، بیشتر از سطح مطلوب باشد، مراکز از شدت فعالیت خود در راستای جمع‌آوری خون می‌کاهند و حتی در مواردی که سطح موجودی بسیار بیشتر از سطح مطلوب باشد، واحدهای خونی اضافی را به مراکز دیگر می‌فرستند و یا با توجه به سپری شدن طول عمر خون، آن‌ها را دورریز می‌کنند.

در شکل 1، نحوه عملکرد یک زنجیره تأمین  خون در صورت وقوع بحران در سه فاز به تصویر کشیده شده‌است. در فاز اول یا فاز پیش از بحران، زنجیره تأمین  در حالتی پایدار است و نرخ عرضه (μ) بیشتر از نرخ مصرف (λ) یا برابر آن است. در صورتی که سطح موجودی کمتر از سطح مطلوب باشد، معمولاً محدودیت‌هایی در پاسخگویی به تقاضای بیمارستان‌ها اعمال می‌شود. در فاز دوم که بعد از وقوع بحران است، تقاضا افزایش می‌یابد و موجودی‌های بیمارستان‌ها نمی‌توانند پاسخگوی نیازها باشند و برای جبران این کمبود، از اهداکنندگان درخواست می‌‌شود که به اهدای خون اقدام کنند. در برخی موارد، قبل از ایام تعطیلات که کاهش اهدای خون انتظار می‌رود و هم‌چنین پیش‌بینی می‌شود که تقاضای خون به دلیل افزایش نرخ تصادفات، افزایش خواهد یافت، از مردم برای اهدای خون فوری درخواست می‌شود. سپس، با توجه به میزان انعطاف‌پذیری زنجیره تأمین  در فاز سوم، وضعیت به حالت پایدار خود باز می‌گردد. (فاز اول)

شکل 1. توازن عرضه و تقاضا در زنجیره تأمین خون در شرایط بحرانی

از این رو که عدم برقراری توازن در زنجیره تأمین خون می‌تواند در آسایش بیماران تأثیرگذار باشد، بنابراین مدیریت مؤثر زنجیره تأمین خون امری ضروری است. همان‌طور که ذکر شد، افزایش در اتلاف خون و هزینه‌های اضافی مرتبط با جمع‌آوری خون، بعد از وقوع بحران ممکن است رخ دهد؛ ولی به این عامل توجه نشده‌است که پس از این دعوت به اهدای همگانی، تعداد واجدین شرایط برای اهدای خون در فاز بعد از بحران با کاهش شدیدی روبه‌رو خواهد شد. به‌عبارت‌دیگر، اهداکنندگان خون در فاز دوم، دیگر قادر به اهدای خون در فاز سوم نخواهند بود و بعد از سپری شدن حداقل فاصله مورد نیاز میان دو اهدای خون متوالی (56 یا 84 روز)، مجدداً مجاز به اهدای خون خواهند شد و از این رو، احتمال وقوع کمبود خون در فاز سوم وجود خواهد داشت. در این مقاله، اثر درخواست فوری خون در میزان دسترس‌پذیری اهداکنندگان مستمر خون و بر میزان انعطاف‌پذیری زنجیره تأمین خون مطالعه شده‌است.

ویژگی‌های اصلی مسئله:

·         در این مقاله، روشی جدید برای مدلسازی اهدای خون توسط اهداکنندگان مستمر ارائه شده‌است که رهنمودهای مهمی را در مدیریت اهدای خون فراهم می‌کند.

·         در این مقاله، اثر درخواست فوری خون در فاز بعد از بحران، بررسی شده‌است و اثر کاهش تعداد اهداکنندگان مستمر خون را در دوره معینی بعد از وقوع بحران، مد نظر قرار داده‌شده‌است و هم‌چنین، استراتژی‌هایی برای مقابله با این کاهش اهدای خون در فاز سوم پیشنهاد شده‌است.

مدلسازی خون‌های اهداشده توسط اهداکنندگان مستمر:

دو منیع اصلی برای اهدای خون در نظر گرفته شده‌است: اهداکنندگان بار اول و اهداکنندگان مستمر. وقتی که درخواستی فوری برای اهدای خون می‌شود، جمع‌آوری خون از اهداکنندگان بار اول و اهداکنندگان مستمر افزایش می‌یابد. بعد از اهدا، هر دو نوع از اهداکنندگان از اهدای خون به مدت T روز منع می‌شوند. این مسئله در ارتباط با اهداکنندگان بار اول چندان حائز اهمیت نیست؛ چون این اهداکنندگان به ندرت برای اهدای خون مجدد اقدام می‌کنند. ولی این دوره‌ی زمانی T روزه، در ارتباط با اهداکنندگان مستمر مهم است و باعث کاهش حجم خون‌های جمع‌آوری‌شده در آینده می‌شود. بنابراین، در این پژوهش اثر درخواست اهدای فوری، در کاهش اهداکنندگان مستمر خون و در کاهش اهدای خون در فاز سوم بررسی شده‌است.

اهداکنندگان مستمر، هنگامی که مجاز به اهدای خون هستند، فرض می‌شود که به طور منظم و با احتمال p که برای اهداکنندگان نختلف متفاوت است، به اهدای خون اقدام می‌کنند. فرض شده‌است که N اهداکننده‌ی خون مستمر وجود دارد و p نیز دارای توزیع احتمالی است. گذار اهداکنندگان مستمر از حالت مجاز برای اهدای خون (حالت A) به حالت معافیت موقت از اهدای خون (حالت R) توسط فرآیند مارکف زمان گسسته فرموله شده‌است. در شکل 2، فرآیند جمع‌آوری خون از اهداکنندگان مستمر نمایش داده شده‌است.

شکل 2. نمایش فرآیند اهدای خون توسط اهداکنندگان مستمر با زنجیره مارکف زمان گسسته 

با توجه به شرایط واقعی، هر اهداکننده بعد از اهدا، به مدت T روز ( معمولاً 84 یا 56 روز که بسته به قوانین انتقال خون در هر کشور می‌تواند متفاوت باشد) از اهدای خون معاف می‌شوند. به‌ عنوان مثال، حالت R₅ در شکل 2 نشان‌دهنده آن است که فرد اهداکننده، 5 روز قبل خون خود را اهدا کرده و تا T-5 روز آینده مجاز به اهدای خون نمی‌باشد. ماتریس گذار برای این زنجیره مارکوف زمان گسسته به صورت زیر است:

در زنجیره مارکوف باید احتمال جریان‌های ورودی به هر حالت با احتمال جریان‌های خروجی از آن حالت باید برابر باشند که به همین دلیل، در زنجیره مارکوف ارائه‌شده، احتمالات در نظر گرفته‌شده برای هر گره از زنجیره مارکوف، دارای توزیع ثابتی است. با در نظر گرفتن این موضوع، معادله مرتبط با هر اهداکننده در حالت مجاز به صورت زیر خواهد بود:

π_j در این رابطه احتمال بودن در حالت j است و با اعمال همین رویکرد برای حالت معاف موقت، خواهیم داشت: 

به‌علاوه می‌دانیم که جمع همه احتمالات برابر یک است. 

با جایگذاری معادله (2) در معادله (1) خواهیم داشت:

بنابراین داریم:

فرض می‌کنیم X پیشامد مربوط به اهدای خون توسط یک اهداکننده مستمر در یک روز معین باشد. بنابراین، احتمال این پیشامد برابر حاصلضرب احتمال مجاز بودن اهداکننده مکرر به اهدای خون و احتمال بازگشت آن اهداکننده خواهد بود.

از این رابطه آشکار است که X تابعی از توزیع برنولی با پارامتر p است. از این پس، احتمال بازگشت اهداکننده i برای اهدای مجدد خون با p_i نشان داده‌می‌شود و N تعداد جمعیتی اهداکنندگان مستمر است که یک عدد ثابت نسبتاً بزرگ فرض می‌شود و L تعدادی از اهداکنندگان مستمر است که در یک روز معین به اهدای خون می‌پردازند.

در این مدل فرض شده‌است که اهداکنندگان بعد از سپری شدن دوره معافیت موقت آن‌ها، مجاز به اهدای خون هستند. با این وجود، در برخی موارد بیماری‌هایی نظیر عفونت مانع از اهدای خون برای چندین دوره می‌شود که این موضوع در مدل، لحاظ نشده‌است. به‌علاوه، فرض شده‌است که اهدای خون توسط یک اهداکننده مستمر، مستقل از اهدای خون توسط سایر اهداکنندگان مستمر است و یک آزمایش برنولی با احتمال اهدا (موفقیت) مشخص است که ممکن است این احتمال برای اهداکنندگان مختلف متفاوت باشد. بنابراین، حجم خون‌های جمع‌آوری‌شده از اهداکنندگان مستمر در یک روز معین (L) تابعی از توزیع پواسون دوجمله‌ای است که به صورت جمع n آزمایش برنولی مستقل با احتمال‌های موفقیت p₁,p₂,…,p_n تعریف می‌شود و امید ریاضی شرطی و واریانس آن نیز به صورت زیر محاسبه می‌شود:

واریانس L، تابعی از امید ریاضی آن و جمعیت کل اهداکنندگان مستمر است و می‌توان گفت که با افزایش امید ریاضی، واریانس نیز افزایش می‌یابد و بنابراین در زنجیره‌های تأمین با ابعاد بزرگ، نوسان زیادی در تعداد اهداکنندگان مستمر انتظار می‌رود.

هم‌چنین، اثبات شده‌است که واریانس L، تابعی صعودی از امید ریاضی آن است و در واقع، این گزاره اثر افزایش احتمال بازگشت اهداکنندگان را در عملکرد زنجیره تأمین بررسی می‌کند. این گزاره نشان می‌دهد که اگر تعداد اهداکنندگان ثابت و احتمال بازگشت آ‌ن‌ها افزایش یابد، امید ریاضی و واریانس تعداد خون‌های جمع‌آوری‌شده از اهداکنندگان مستمر افزایش می‌یابد. با این جود، برای دستیابی به یک سطح متوسط معین در میزان خون‌های اهدایی توسط اهداکنندگان مستمر، افزایش در احتمال بازگشت اهداکنندگان مؤثرتر از افزایش در جمعیت اهداکنندگان است. در توجیه این موضوع می‌توان بیان کرد که واریانس خون‌های جمع‌آوری‌شده توسط اهداکنندگان مستمر، در صورت افزایش احتمال بازگشت کمتر از موقعی است است که تصمیم‌گیرندگان قصد در جذب تعداد بیشتری از اهداکنندگان مستمر دارند.

اثبات شده‌است که با افزایش احتمال بازگشت اهداکنندگان، تعداد جمعیت مورد نیاز از اهداکنندگان مستمر برای دستیابی به یک امید ریاضی معین (E(L)) کاهش می‌یابد و هم‌چنین، واریانس حجم خون اهدایی توسط اهداکنندگان مستمر ((var(L) نیز کاهش می‌یابد. بنابراین با به‌کارگیری سیاست‌هایی برای افرایش احتمال بازگشت اهداکنندگان، نیاز به جذب اهداکنندگان مستمر جدید کاهش می‌یابد و عملکرد زنجیره تأمین با کاهش نوسانات در تعداد خون‌های جمع‌آوری‌شده در هر روز بهبود می‌یابد.

سازمان‌های خون از اهمیت اهداکنندگان، به‌خصوص اهداکنندگان مستمر خون آگاه هستند و از این رو، به دنبال راهکارهایی برای ترغیب اهداکنندگان به‌منظور افزایش احتمال بازگشت آن‌ها برای اهدای خون هستند. هم‌چنین اثبات شده‌است که تلاش در راستای افزایش احتمال بازگشت اهداکنندگانی که احتمال بازگشت آن‌ها کم است، بهبود بیشتری در عملکرد زنجیره تأمین دارد.

 هم‌چنین اثبات شده‌است که اگر احتمال بازگشت، تابعی از توزیع بتا باشد ((p ∼ Beta(α, β) و N نیز عدد بزرگی باشد که جمعیت اهداکنندگان را نشان‌ می‌دهد، در این صورت حجم خون اهداشده توسط اهداکنندگان مستمر خون، دارای توزیع نرمال خواهد بود.

که در آن

به‌علاوه، اگر احتمال بازگشت تابعی از توزیعی مانند (fˆ(p باشد، امید ریاضی و واریانس L به صورت زیر محاسبه خواهدشد:

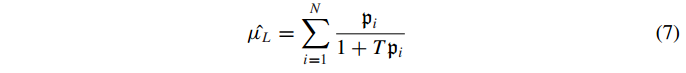
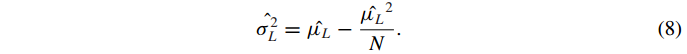
که در آن p₁,p₂,…,p_N نمونه‌های تصادفی تولیدشده از توزیع (fˆ(p هستند.

مدلسازی اهدای خون در فاز بعد از بحران:

در بخش قبلی، اهدای خون در شرایط عادی بررسی شد و در این گام، اثر درخواست فوری خون در عملکرد زنجیره تأمین خون بررسی می‌شود.‌ هنگامی که درخواستی فوری برای اهدای خون صادر می‌شود، حجم خون‌های اهداشده افزایش می‌یابد و از این رو، تعداد زیادی از اهداکنندگان مستمر در فاز سوم، برای مدت معینی از اهدای خون معاف می‌شوند. فرض می‌کنیم که E(L_uc) امید ریاضی تعداد اهداکنندگان مستمری باشد که در صورت درخواست فوری خون، اقدام به اهدای خون می‌کنند. بنابراین خواهیم داشت:

 

که در آن γ ضریبی است که نشان‌دهنده افزایش در حجم اهدا است. پس از اتمام جمع‌آوری خون برای درخواست فوری، جمعیت اهداکنندگان مستمری که مجاز به اهدای خون هستند، برای T روز آتی از رابطه‌ زیر محاسبه می‌شود:

که در آن l تعداد روزهایی است که برای پاسخ‌گویی به درخواست فوری، خون جمع‌آوری می‌شود. بنابراین، برای محاسبه حجم خون جمع‌آوری‌شده توسط اهداکنندگان مستمر در فاز سوم، باید N’ جایگزین N در معادله (7) شود.

اگر p دارای توزیع بتا باشد، امید ریاضی تعداد اهداکنندگان مستمر خون که مجاز به اهدای خون در فاز سوم بعد از درخواست فوری خون هستند، از رابطه زیر به‌دست خواهدآمد:

 

این شرایط بر زنجیره تأمین حاکم خواهد بود تا زمانی که اهداکنندگان مستمر خون، مجدداً مجاز به اهدای خون شوند. از معادله (11) می‌توان نتیجه گرفت که در T-(l-1) روز اول از فاز سوم، به تعداد k واحد خونی از حجم عرضه خون در هر روز کاسته می‌شود که از رابطه زیر محاسبه می‌شود:

میزان کل کاهش در اهدای خون در فاز سوم، در صورتی که احتمال بازگشت دارای توزیع بتا باشد، از رابطه‌ی زیر به‌دست می‌آید:

و اگر احتمال بازگشت دارای توزیع بتا نباشد، میزان کاهش اهدای خون در طول فاز سوم توسط فرمول زیر محاسبه می‌شود:

احتمال بازگشت هر اهداکننده را می‌توان از طریق فرمول زیر برآورد کرد:

نتایج:

برای ارزیابی مدل از مثال‌های عددی مختلفی استفاده شده‌است و نتایج آن‌ها مورد ارزیابی قرار گرفته‌است. نحوه عملکرد مدل در برابر ضریب اهدای خون  (θ) و طول مدت زمان فراخوان برای اهدای فوری خون (l) آنالیز شده‌است. نتایج نشان‌دهنده آن است در مقدار θ و l، حجم خون‌های جمع‌آوری‌شده توسط اهداکنندگان مستمر خون با کاهش بیشتری مواجه می‌شوند. به عبارت دیگر، افزایش در مقدار θ و l منجر به اهدای بیشتر خون در فاز دوم و متعاقباً منجر به ممنوعیت تعداد بیشتری از اهداکنندگان مستمر از اهدای خون در فاز سوم می‌شود.

به‌علاوه، با توجه به مدل مشخص است که مدت زمان معافیت موقت اهداکنندگان مستمر (T) بر میزان کاهش اهدای خون بعد از درخواست فوری خون مؤثر است. این مدت زمان توسط سازمان‌های انتقال خون در هر کشور تعیین می‌شود و می‌تواند برای کشورهای مختلف، متفاوت باشد. نتایج نشان‌دهنده آن است که کاهش طول این دوره، میزان کاهش در حجم خون‌های جمع‌آوری‌شده در فاز سوم افزایش می‌یابد. در توجیه این موضوع می‌توان بیان کرد که با توجه به رابطه (3) افزایش در طول این دوره منجر به کاهش احتمال مراجعه یک اهداکننده برای اهدای خون در یک روز معین می‌شود و نرخ اهدای کمتر در فاز دوم، از میزان کاهش در حجم خون‌های جمع‌آوری‌شده در فاز سوم می‌کاهد. هم‌چنین T و نرخ کاهش روزانه در اهدای خون دارای رابطه‌ای غیرخطی دارند و کاهش یک روز از مدت T وقتی که T مقادیر کمی را اختیار کرده‌است، اثرات منفی بیشتری در عملکرد زنجیره تأمین بر جای می‌گذارد نسبت به مواقعی که T دارای مقادیر بیشتری است.

هم‌چنین، با توجه به مدل می‌توان نتیجه گرفت که در صورتی که احتمال بازگشت اهداکننده، تابعی از توزیع بتا باشد، در تحلیل نحوه تأثیر احتمال بازگشت بر زنجیره تأمین می‌توان بیان کرد که افزایش پارامتر α از توزیع بتا باعث افزایش میانگین تعداد اهداکنندگان مستمر در فاز دوم می‌‌شود که این عامل نیز، میزان کاهش در نرخ خون‌های اهداشده در فاز سوم را افزایش می‌دهد.