روشی پیشرفته برای مدیریت زنجیره تامین خون تحت اختلال و عدم قطعیت(مقاله دوم)

چکیده:

مدیریت زنجیره تامین خون، درگیر با تعدادی از چالش های مستقیم مانند بی نظمی در عرضه و تقاضای خون، تعدد فرآورده های خونی، طول عمر کوتاه و فساد پذیری آن ها میباشد. علاوه بر این، مواجهه با خطرات ناشی از بلایای طبیعی یا حوادث وابسته به انسان مانند اعتصاب کارگری، مشکلات اقتصادی و... نیز باعث ایجاد عدم قطعیت در داده برای طراحی و مدیریت شبکه زنجیره تامین خون شده است. در این مقاله به یک چشم انداز پیشرفته شامل یک سیاست پیشگیرانه دو مرحله ای که ریسک ایجاد اختلال را با روش ترکیبی با استفاده از فرآیند تحلیل سلسله مراتبی فازی و منطق خاکستری برای تعیین تسهیلات اضافه خون برای تولید و کاهش وقفه می پردازد. علاوه بر این، یک فرمول  p_استوار  برای کنترل قابلیت اطمینان شبکه تحت سناریوهای اختلال با حداقل هزینه ارائه شده است. همچنین برای محافظت از شبکه در برابر عدم قطعیت، از روشی تلفیقی مبتنی بر یک رویکرد توسعه یافته فازی استفاده شده است. اعتبار و کاربردی بودن مدل و راه حل پیشنهادی به همراه قابلیت اطمینان شبکه توسط یک مطالعه موردی واقعی در ایران بررسی شده است.

کلمات کلیدی: زنجیره تامین خون، فرآیند تحلیل سلسله مراتبی فازی، منطق خاکستری، ریسک اختلال، برنامه ریزی استوار فازی

 مقدمه:

طراحی شبکه زنجیره تأمین خون (BSCND) به تصمیمات مهم استراتژیک با پیامدهای بلند مدت در مدیریت زنجیره تامین خون می پردازد. در واقعیت، یکی از کاربردی ترین موضوعات مربوط به طراحی و برنامه ریزی شبکه، خطرات تهدید کننده قابلیت اطمینان شبکه ها است. به خصوص شبکه هایی که دارای ساختار تأسیساتی متمرکز هستند (مانند شبکه مربوطه در این مطالعه که معمولاً کل سیستم توسط یک مرکز خون منطقه ای منفرد (RBC) اداره می شود که وظیفه غربالگری خون، کسری و توزیع آن را بر عهده دارد)، در معرض خطر هستند. .

ریسک وجود عدم هماهنگی بین سیستم و تقاضاها که می تواند به عنوان عدم قطعیت نیز تعریف شود ، موضوع دیگری است که مورد توجه محققان قرار گرفته است. به عنوان مثال، ظهیری و پیشوائی (2017) یک مساله زنجیره خون در محیط عدم قطعیت را مورد بررسی قرار داده و برای مقابله با عدم قطعیت معرفتی ذاتی پارامترهای مدل، از یک روش برنامه ریزی فازی استوار استفاده کرده اند. میتوان یک مساله طراحی شبکه چند دوره دو مرحله ای برای تامین خون در شرایط بحران در نظر گرفت. تقاضا برای فرآورده های خونی از جمله پلاکت ها و پلاسما متغیر تصادفی فرض می شود و تحت سناریوهای مختلف در نظر گرفته میشود. برای پاسخ به ماهیت تصادفی پارامترها، میتوان از یک روش بهینه سازی استوار استفاده کرد. فاصله بین اهداکنندگان و تسهیلات خون، تجربه اهداکنندگان و تبلیغات در مراکز خونی برای تدوین کارکردهای اهداکنندگان در نظر گرفته شده است. در این تحقیق از یک روش ترکیبی استوار_فازی برای بهره مندی از مزایای هر دو استفاده شده است.

 متدولوژی حل

محیط غیر قطعی و اختلالات دو منبع خطر عمده هستند که در مورد بلایای طبیعی بیشتر برجسته می شوند. برای پرداختن به این دو عامل بروز ریسک، این مقاله یک روش پیشرفته مبتنی بر یک رویکرد دو مرحله ترکیبی را برای اولین بار پیشنهاد کرده است.

 در مرحله اول، یک چارچوب پیشگیرانه دو مرحله ای را برای مقابله با خطر اختلال با رویکردی نوآورانه ارائه کرده است که در آن تسهیلات تکمیلی (SBF) به عنوان گزینه های پشتیبان برای جلوگیری از به تعویق افتادن تولید و قطع شبکه و در نظر گرفتن  یک روش p-استوار برای مدیریت قابلیت اطمینان شبکه ارائه شده است. در مرحله دوم، یک رویکرد ترکیبی استوار_فازی کارآمد برای مواجه با ریسک عملیاتی ناشی از عدم اطمینان داده های ورودی طراحی شده است.

 مقابله با خطر اختلال:

از آنجایی که هر دو تصمیمات استراتژیک و تاکتیکی را در شبکه مربوطه اتخاذ شده است، مدل p-robust به عنوان یک فرمول دو مرحله ای ارائه می شود:

مرحله اول:

ارزیابی معیار های کیفی  مکان های کاندید با روش AHP-GRA

مرحله دوم:

هدف، طراحی و برنامه ریزی شبکه زنجیره تامین خون با قابلیت اطمینان بالا برای تهیه کافی محصولات خون در سناریوهای اختلال میباشد.

مقابله با ریسک عملیاتی

ماهیت پویا طراحی  شبکه زنجیره تامین خون، باعث عدم اطمینان زیادی در اکثر داده های ورودی مانند میزان عرضه خون و میزان تقاضای خون، هزینه های تاسیس تسهیلات خون، هزینه حمل و نقل و غیره می شود. تقریباً در کلیه تصمیم گیری های بلند مدت از جمله تصمیم گیری در مورد مکان یابی، به کارگیری یک روش استوار ضروری به نظر می رسد. در چنین تصمیماتی، که حساسیت بالایی به پارامترهای تصادفی دارند، اتخاذ رویکرد مناسب بسیار مهم است زیرا تغییر تصمیمات طولانی مدت ساده نیست.

بررسی عدم قطعیت در پارامتر ها

بیشتر پارامترهای موجود در مساله طراحی شبکه زنجیره تامین خون مورد بررسی  با درجه بالایی از عدم اطمینان همراه هستند که این به دلیل ماهیت پویا مسئله  به عنوان مثال، نوسانات احتمالی در مقادیر پارامترها در افق بلند مدت می باشد.

در چنین شرایطی، استواری راه حل نهایی از اهمیت ویژه ای برخوردار است، زیرا تصمیم گیری در مورد مکانیابی و تخصیص و تعیین ظرفیت در یک افق بلند مدت قابل تغییر نیست. با در نظر گرفتن این واقعیت ها، برای مقابله با پارامترهای غیر قطعی، یک رویکرد HRPP جدید در این مقاله تدوین شده است.

برنامه ریزی استوار

در اکثر مسائل در سطح استراتژیک، تصمیم گیرنده ها تمایل دارند یک تصمیم پایدار بگیرند که هم از نظر شدنی بودن و هم بهینگی دارای استواری باشد. استواری شدنی بودن بدان معنی است که راه حل باید برای تقریباً همه مقادیر ممکن پارامترهای غیر قطعی امکان پذیر باشد و استواری بهینگی به معنای این است که مقدار تابع هدف باید نزدیک به مقدار ایده ال باشد و یا حداقل انحراف را از مقدار ایده ال برای (تقریبا) همه مقادیر ممکن پارامترهای غیر قطعی داشته باشد.

رویکردهای برنامه ریزی استوار را می توان به سه گروه طبقه بندی کرد :

الف) رویکرد بدبینانه سخت  (ب) رویکرد بدبینانه نرم   (ج) رویکرد واقع بینانه.

در روش بدبینانه سخت،  فرض می شود که همه پارامترهای غیرقطعی بدترین مقدار خود را بگیرند،که در بین این سه رویکرد به عنوان بدبینانه ترین حالت (یعنی محافظه کارانه) شناخته می شود. نقطه ضعف اصلی این روش این است که روی استواری شدنی بودن متمرکز شده و بنابراین کمترین استواری بهینگی را به دست می دهد. بنابراین به نظر می رسد فقط برای شرایط اضطراری و نظامی مناسب است. در عوض، این روش نیاز به اطلاعات اضافی درباره توزیع امکان یا احتمال پارامترهای غیرقطعی را از بین می برد. رویکرد بدبینانه نرم نسبتاً منعطف  تر از رویکرد اول است زیرا سعی می کند بدترین مقدار تابع هدف  را کمینه کند، در حالی که همه ی محدودیت ها را در بدترین حالت خود برآورده نمی کند. سرانجام، رویکرد واقع بینانه تلاش می کند بین استواری راه حل به دست آمده و استواری هزینه تعادل برقرار کند (به عنوان مثال ، دارای منطق هزینه منفعت است و بنابراین برای زمینه های تجاری مناسب است).

مدل PCCP

برنامه ریزی ریاضی فازی (FMP) قادر است به طور مناسب عدم قطعیت شناختی در داده ها و انعطاف پذیری در اهداف یا محدودیت ها را کنترل کند. FMP را می توان به دو دسته اصلی طبقه بندی کرد: (الف) برنامه ریزی امکانی pp) ( ب ) برنامه ریزی منعطف.  برنامه ریزی امکانی برای مواجهه با عدم قطعیت شناختی داده ها به کار برده می شود که توزیع امکان آن با توجه به داده های موجود یا نظر  DM  و یا با کمک خبره تعیین می شود. برنامه ریزی منعطف برای مقابله با عدم قطعیت در محدودیت (های) نرم و یا در مقدار تابع هدف به کار برده می شود.

برنامه ریزی امکانی محدودیت شانس pccp (محدودیت هایی با عدم قطعیت در داده ها)، یک روش شناخته شده PP  می باشد که برای مقابله  با  داده های امکانی در سمت راست و چپ به کار برده می شود. در این رویکرد  DM  یک حداقل سطح اطمینان (α)  را به عنوان حاشیه امنیت سطح ارضای  هر محدودیت شانس امکانی  در نظر می گیرد. پیمانه امکان (pos)  و الزام (nes) دو پیمانه شناخته شده فازی برای براورده سازی چنین اطمینان هایی  در مدل های pccp  می باشد . پیمانه امکان خوش بینانه ترین سطح احتمال وقوع پارامترهای امکانی را نشان می دهد در حالیکه پیمانه nes  بدبینانه ترین نگرش DM  را نشان می دهد.

عدد فازی مثلثی را در نظر بگیرید،که تابع عضویت آن به صورت زیر مشخص می شود:

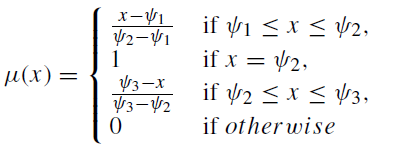
برای  α> 0.5  معادل قطعی توابع عضویت در پیمانه های الزام و امکان به شرح زیر محاسبه می شود :

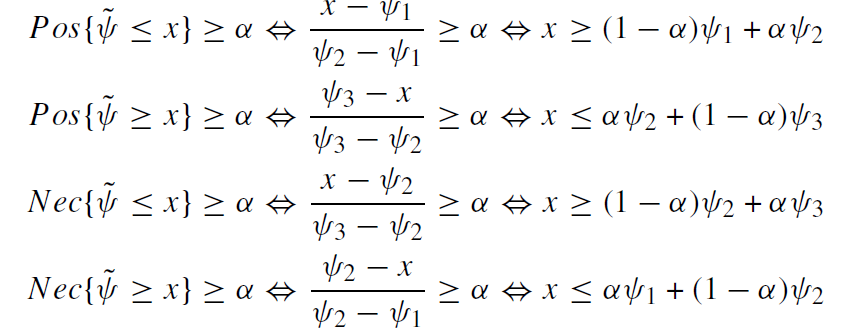
 همچنین برای ѱ₁ > 0 ارزش انتظاری پیمانه های ذکر شده به طریق زیر محاسبه می شود.

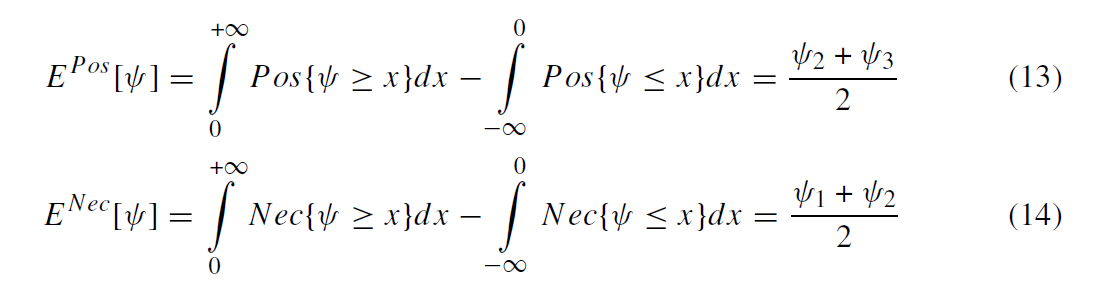
 اقدامات فوق بسیار افراطی است اگرچه در واقعیت، تصمیم گیر ها ممکن است نسبت به داده های احتمالی رفتار بی طرف تری داشته باشند.  بر این اساس، برای رفع این مشکل، یک روش فازی اصلاحی به نام پیمانه  Me  توسط Xu و Zhou (2013) معرفی شده است. تصمیم گیرها با استفاده از پیمانه Me قادر به انتخاب هر نوع ترکیب محدب در فاصله پیمانه های Pos و Nec هستند. با تغییر مقدار γ در فاصله  [0.1]، DM ها می توانند ترکیبات مورد نظر خود را بدست آورند. از این نظر:

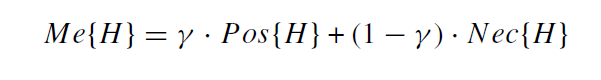
  ·      براساس نظر بدبینانه ترین DM ها(γ = 0) ، پیمانهMe برابر است با معیارNec ، که حداقل سطح احتمال وقوع رویداد احتمالی H را به دست می دهد.

·      براساس نظر خوشبینانه ترین DM ها(γ = 1) ، پیمانه Me برابر است با معیارPos ، که حداکثر سطح احتمال وقوع رویداد احتمالی H را به دست می دهد.

براساس Xu and Zhou (2013) ، برای   α ≥ 0.5 پیمانه Me و مقدار پیش بینی شده ˜ψ به عنوان برای ψ1 ≥ 0 تعریف شده است.

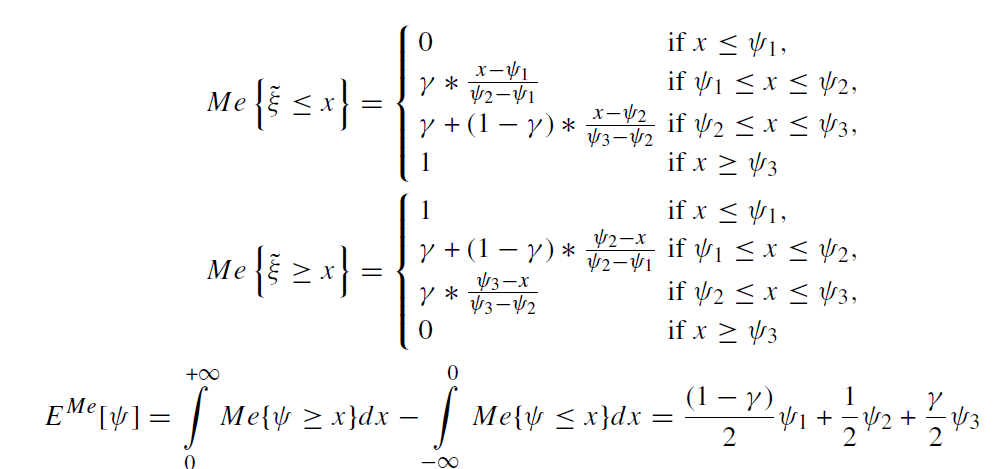
در موارد بحرانی مانند مسائل سیستم های سلامت و همچنین مسائلSCND ، تصمیم گیرندها برای اطمینان از شانس بالا برای برقراری محدودیت های احتمالی، تمایل دارند که یک نگرش بدبینانه اتخاذ کنند. در نتیجه، γ مقادیر کمتر از 0.5 را برای دستیابی به اقدامات Nec برای حمایت از رویکرد بدبینانه تصمیم گیرمی گیرد. بنابراین،  پیمانه Me به روابط زیر تبدیل می شود:

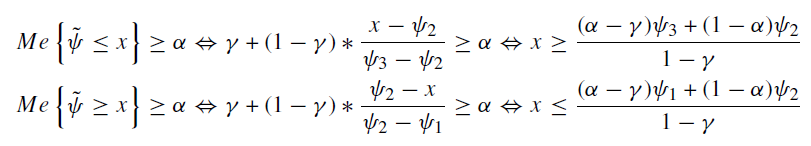
 مدل پایه  (BPCCP)PCCP

در مدل زیر، F , G , B , E   به  ترتیب، هزینه های ثابت،هزینه های متغیر، میزان تقاضا و میزان عرضه که دارای عدم قطعیت می باشند.

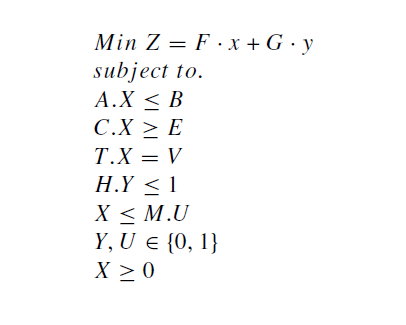
برای تبدیل مدل BPCCP ، به مدل قطعی، از عملگر ارزش انتظاری برای تبدیل تابع هدف امکانی  به همتای قطعی  خود استفاده می شود، و همچنین پیمانهMe  برای مقابله با محدودیت های شانس احتمالی شامل پارامترهای غیرقطعی به کار برده می شود.  در اینجا ، توزیع امکان مثلثی را برای مدل سازی پارامترهای غیرقطعی به کار میبریم:

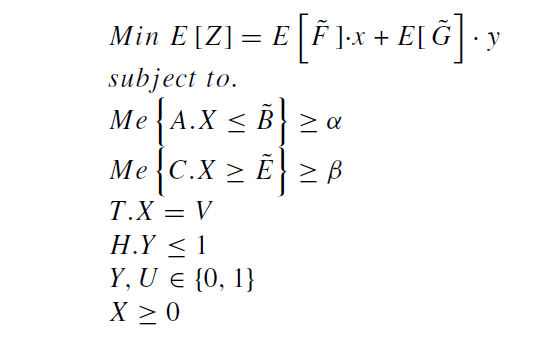
  رویکرد ترکیبی برنامه ریزی استوار امکانی ( HRPP)

اگرچه مدل  BPCCPبه طور مناسبی می تواند با پارامترهای غیرقطعی مقابله کند، اما  از آنجا که به انحراف مقدار تابع  هدف از مقدار مورد انتظار خود حساس نیست، انحراف در مقدار پارامترهای غیرقطعی در برخی از حالات واقعی می تواند ریسک زیادی را به تصمیم گیر  تحمیل کند. از این رو استفاده از رویکردهای برنامه ریزی فازی و استوار توصیه می شود تا هم از مزایای فازی و هم از مزایای رویکرد استوار بهره برد. در ادامه، یک رویکرد HRPP  نوین معرفی می شود که  شامل سه رویکرد واقع گرایانه, یعنی HRPP-I ، HRPP-II  ،   HRPP-III و یک رویکرد سختگیرانه (یعنی HWRPP   ) می باشد، که  در این ادامه چهار نوع HRPP بر اساس پیمانه  Me توضیح داده شده است.

 نوع اول ، یعنی HRPP-I به شرح زیر است:

بر پایه پیمانه Me  , مدل  HRPP-I به صورت زیر تعریف می شود:

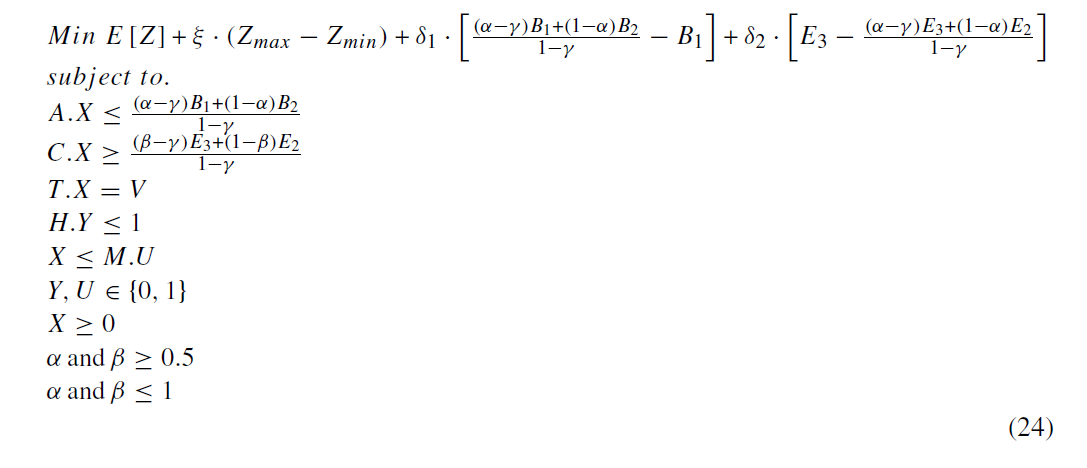
بخش اول، مقدار مورد انتظار z (عملکرد مورد انتظار تابع هدف) را بهبود می بخشد. بخش دوم استواری بهینگی جواب نهایی را با مینیمم کردن فاصله بین حداکثر و حداقل مقادیر تابع هدف کنترل می کند. که تابع هدف حداکثر و حداقل به شرح زیر تعریف می شوند:

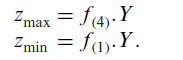
بخش سوم و چهارم، استواری شدنی بودن جواب نهایی را با مینیم کردن اختلاف مقدار سمت راست محدودیت ها از بدترین مقدارشان کنترل می کند.

هنگامی که انحراف تابع  هدف از مقدار مطلوب مورد انتظار آن (یعنی بیش از حد یا زیر مقدار مورد انتظار) مهم باشد ، تابع هدف HRPP-I به فرمول زیر تغییر می کند و مدل HRPP-II شکل می گیرد و مورد استفاده قرار می گیرد. محدودیت ها تغییر نمی کند( همان محدودیت های HRPP-I  )

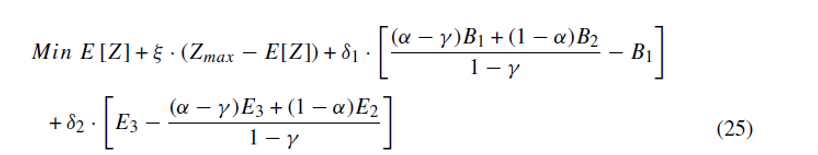
اما، هنگامی که DM ها نسبت به انحراف از مقدار مطلوب مورد انتظار تابع هدف حساسیت کمتری دارند  به جای HRPP-II تابع هدف زیر تعریف می شود که HRPP-III را با همان محدودیت هایی مانند HRPP-I تشکیل می دهد.

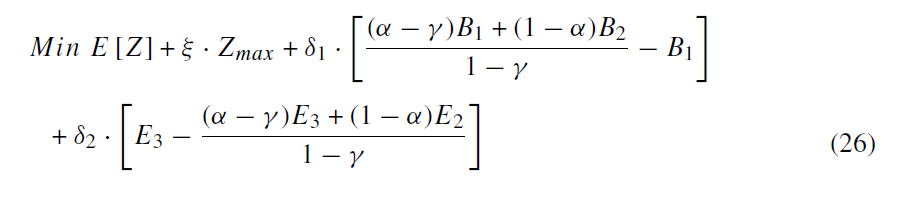
 از طرف دیگر، در رویکرد بدبینانه سخت، راه حل به دست آمده باید حداکثر استواری موجه بودن را داشته باشد، در حالی که DM تلاش می کند تا بدترین مقدار  تابع هدف را نسبت به همه حالات ممکن پارامترهای غیرقطعی بهبود بخشد. hardworst-case robust Programming (HWRP)  بیشتر بر استحکام امکان پذیری تأکید می کند و استحکام بهینه ای ضعیف را به دست می آورد. این رویکرد محافظه کارانه به شکل زیر است:

اگرچه مدل فوق صرفا از بدترین حالت (به جای فراهم آوردن توزیع امکان) پارامترهای غیر قطعی بهره می برد، اما به تابع هدف توجه زیادی نمی کند و ضعیف ترین قدرت مطلوب را در مقایسه با سه مدل قبلی نشان می دهد.

مهم ترین مزیت این رویکرد اینست که به تابع توزیع امکان پارامترهای غیرقطعی نیاز ندارد اما از طرف دیگر پایین ترین سطح استواری بهینگی را در بین مدل های ارائه شده دارد.

 تعریف مسئله

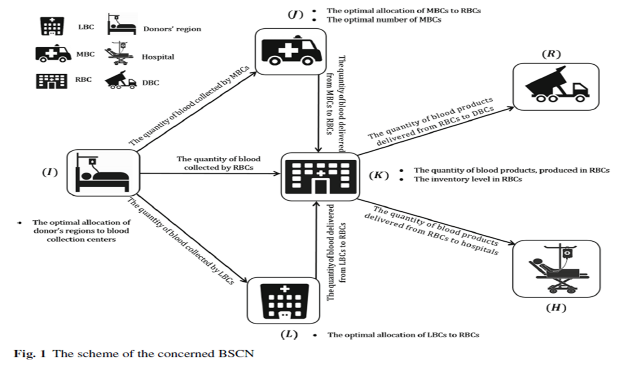
شبکه زنجیره تأمین در نظر گرفته شده، یک شبکه زنجیره تأمین خون چند محصوله است که از مناطق اهداکننده خون، مراکز خون محلی(LBCs) ، مراکز خون متحرک(MBC) ، مراکز خون منطقه ای (RBCs) و بیمارستان ها تشکیل شده است. این شبکه همچنین شامل مراکز خونی دفع (DBCs) برای خون غیر قابل استفاده است. همانطور که در شکل زیر نشان داده شده است، در این شبکه، خون از اهدا کنندگان به بیماران در طی یک روند پی در پی جریان می یابد. این فرآیند توسط خون جمع آوری شده از اهدا کنندگان خون به طور مستقیم از طریق RBCs یا از طریق MBC و LBC صورت می گیرد که واحدهای جمع آوری شده را به RBCs می فرستند تا روند غربالگری را شروع کنند. MBC و LBC به عنوان نقاط انتقال عمل می کنند و از نظر ظرفیت، تجهیزات، هزینه نصب و غیره از یکدیگر متمایز می شوند. RBCs وظیفه تهیه فرآورده های خونی بیمارستان ها را بر عهده دارند. برای انجام این کار، بعد از آزمایش و غربالگری، واحدهای خونی قابل استفاده وارد فرآیند تولید می شوند و به چندین فرآورده فرعی (به عنوان مثال، گلبول های قرمز، پلاسما و پلاکت) تجزیه می شوند. فرآورده های خونی سپس در شرایط ذخیره سازی مربوطه در RBCs  ذخیره می شوند تا در اسرع وقت به بیمارستان ها توزیع شوند. علاوه بر این، خون غیر قابل استفاده (شامل خون های  غیر قابل استفاده و همچنین واحدهای خونی منقضی شده در RBCs ) باید به DBCs ها منتقل شوند

مفروضات:

در شبکه در نظر گرفته شده، از استراتژی جمع آوری خون تک منبعه سه سطحی استفاده شده است. محل LBCs ، RBCs، بیمارستان ها و DBCs از پیش مشخص است. برای هر فرآورده خونی، یک طول عمر مشخص در نظر گرفته شده است.

BSC در نظر گرفته شده در محیط غیر قطعی عمل می کند که میزان تأمین خون، تقاضا و هزینه های شبکه نقش پارامترهای تصادفی را دارند که با استفاده از یک رویکرد استوار فازی کارا در نظر گرفته شده اند. با توجه به توضیحات فوق، در این مقاله به دنبال به تعیین تعداد و محل بهینه مراکز خونی سیار و همچنین مقدار خون و فرآورده های فرعی آن با هدف انتقال از یک مرکز به محل دیگر در سراسر شبکه تعیین می شود. هزینه ها  شامل ( هزینه تأسیس و راه اندازی مراکز خونی سیار و هزینه های تولید، حمل و نقل، موجودی و انقضاء) می باشند.

مدل پیشنهادی قطعی

تابع هدف به دنبال به حداقل رساندن کل هزینه شبکه در حالت اسمی(s0) ، یعنی سناریویی که در آن هیچ گونه اختلال رخ نمی دهد، می باشد. هزینه های شبکه شامل هزینه های عملیاتی درMBC ، LBC و RBC ، هزینه حمل و نقل کل خون از MBC و LBC بهRBCs ، هزینه حمل و نقل فرآورده های خونی از RBCs به بیمارستان ها و محصولات منقضی شده خون از RBCs بهDBCs، هزینه های نگهداری موجودی درRBC ، هزینه های تولید فرآورده های خونی درRBCs ، و هزینه های متحرک MBC  میباشد.

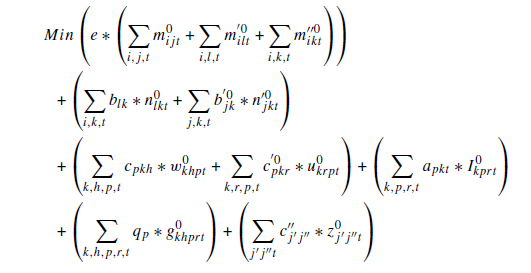
در محدودیت اول یک  حد بالایی برای هزینه شبکه تحت هر سناریو تعیین می شود.

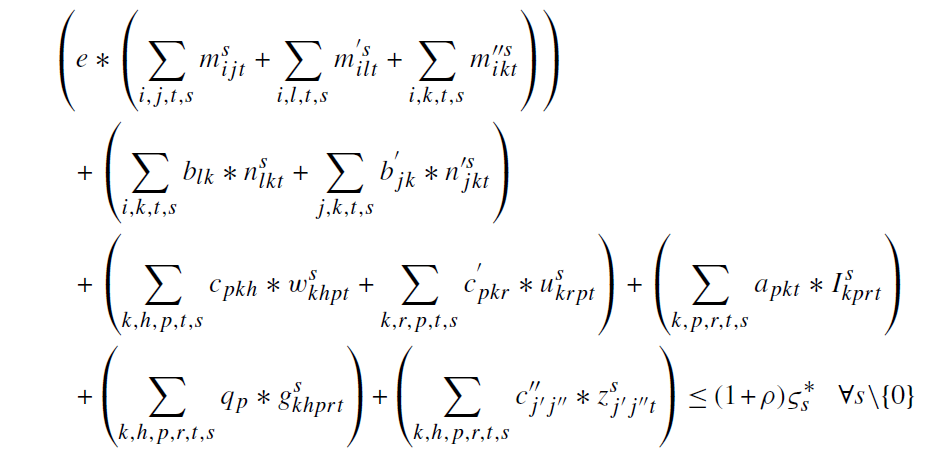
محدودیت های  2و 3 نشان می دهند که فقط یک MBC، می تواند در هر دوره به مکان کاندید دیگری منتقل شود.

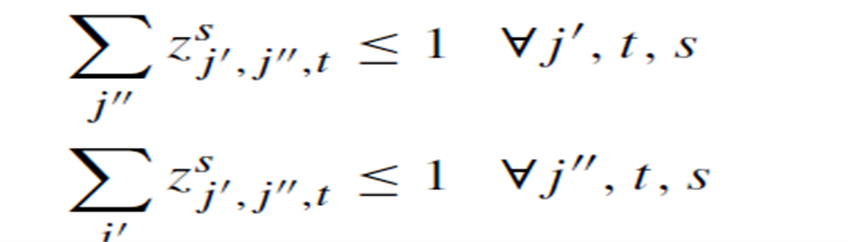
محدودیت 4 : جابجایی یک MBC را در دو دوره پی در پی تنها در صورتی که در دوره قبلی در مکان قبلی بوده باشد امکان پذیر می کند.  تعداد MBC های مورد نیاز در هر دوره نشان داده شده است.

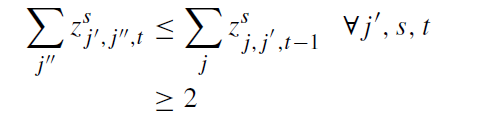
محدودیت 5: به این معنی است که منطقه هر اهدا کننده را می توان به یکLBC ، یک MBC یا RBC اختصاص داد.

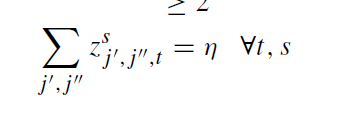
در 6 محدودیت بعدی یعنی 7 تا 11، مسافت طی شده بین مناطق اهدا کننده و MBC ها، مناطق اهدا کننده و LBC ها، مناطق اهدا کنندگان و RBC ها، MBC ها و RBC ها و LBC ها و RBC ها را به ترتیب محدود می کند.

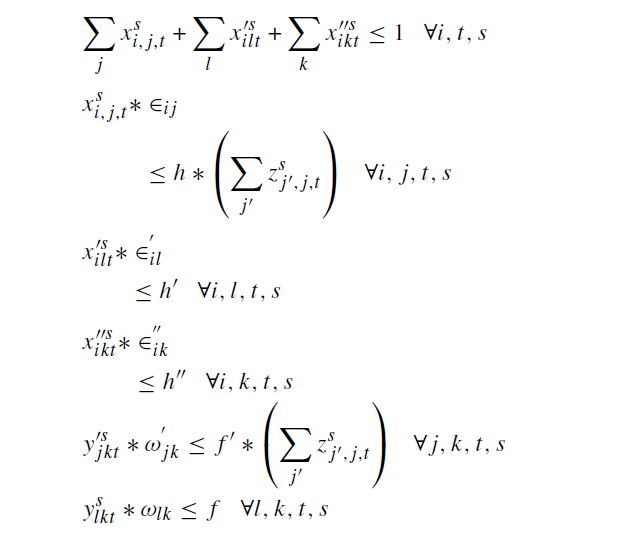
محدودیت 12 و 13: دلالت بر این دارد که هر MBC و LBC را می توان به RBC اختصاص داد:

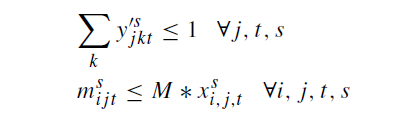
محدودیت های  14_16: فقط در صورتی که مناطق اهدا کننده به این مراکز جمع آوری خون اختصاص یافته باشند ، در هر دوره به ترتیب در LBCs ، MBC  یاRBC ، اهدا خون انجام می شود.

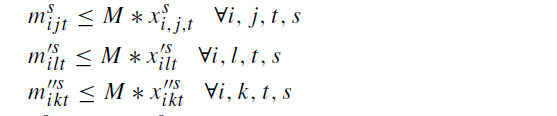
محدودیت های 17 و 18:  تضمین می کنند که انتقال خون فقط در صورت اختصاص MBC یا LBC به RBCs امکان پذیر خواهد بود.

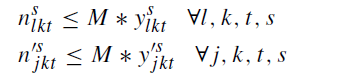
محدودیت19:  حداکثر مقدار خون کامل تهیه شده در هر دوره را تعیین می کند.

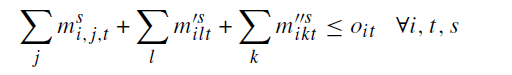
محدودیت های 20_22: حداکثر ظرفیت هر MBC ، LBC و RBC  نشان میدهد:

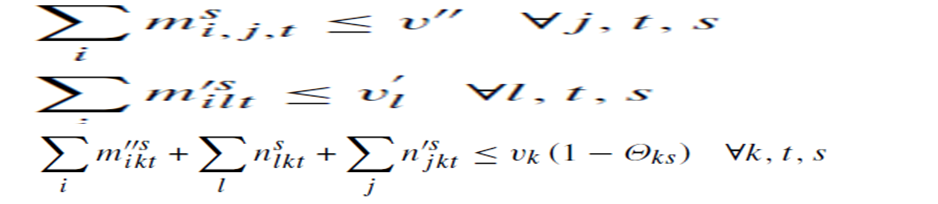
محدودیت های 23 و 24: تعادل جریان بینMBC ها و LBC ها  را نشان میدهد:

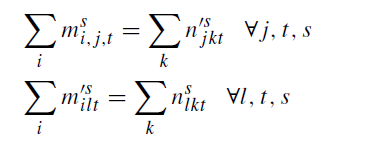
 محدودیت 25: تجزیه خون به هر محصول در گلبولهای قرمز را نشان میدهند.

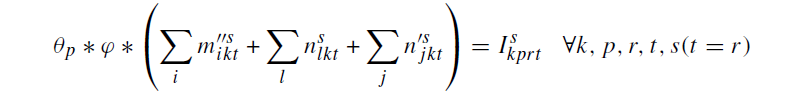
 محدودیت 26 و 27: معادلات موجودی را برای هر RBC در هر دوره بیان میکند.

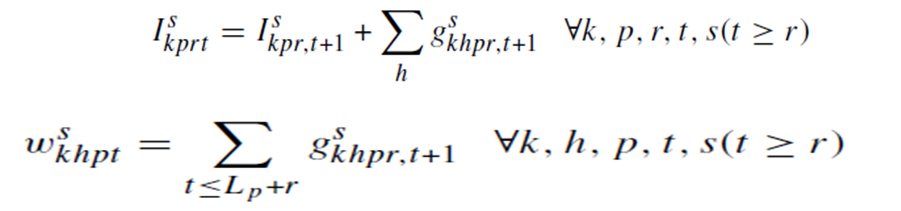
محدودیت 28: اجازه می دهد تا محصولات خونی منقضی شده از RBCs به سمت DBCs منتقل شوند.

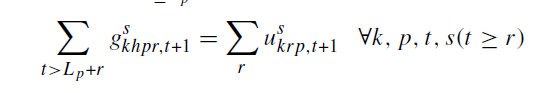
محدودیت 29: ارضای تقاضا برای هر بیمارستان در هر دوره را تضمین می کند.

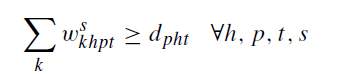
و محدودیت های 30 و 31: نشان دهنده نوع متغیر ها میباشد.

اجرا و ارزیابی مدل:

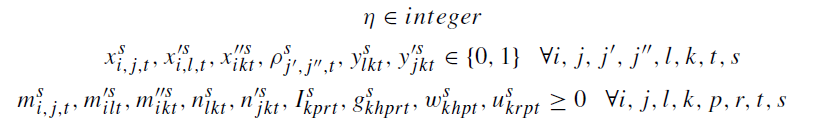
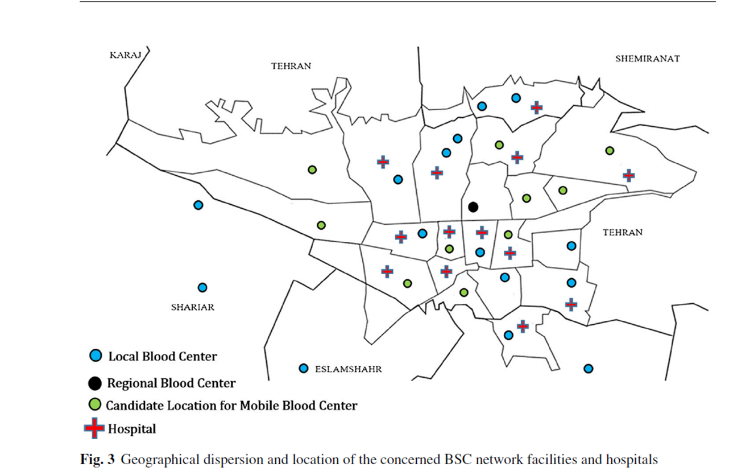
در این بخش،  مطالعه موردی واقعی به تفصیل برای نشان دادن کاربرد و اعتبار مدل پیشنهادی و راه حل آن ارائه شده است. در این مقاله شبکه زنجیره تامین خون تهران برای بهبود شبکه موجود از طریق طراحی و برنامه ریزی کارآمدتر مورد استفاده قرار گرفته است. علاوه بر این، دانش متخصصان و اسناد معتبر از سازمان انتقال خون ایران (IBTO) و شهرداری تهران سه منبع اصلی هستند که برای جمع آوری داده های مورد نیاز برای مطالعه موردی از آنها استفاده شده است. این داده ها شامل هر دو ارزش فنی و پولی هستند. به عنوان مثال، مقدار متوسط ​​خون در هر منطقه اهدای خون و تقاضای تصادفی از هر بیمارستان، به همراه داده های مربوط به عمر مفید خون و فرآورده های فرعی آن و غیره از داده های فنی موردنیاز است. همچنین، هزینه های زنجیره تأمین شامل هزینه تأسیس، هزینه عملیاتی، هزینه تولید و موجودی انبار، هزینه حمل و نقل و غیره داده های پولی است که با دلار اندازه گیری می شود.

در مطالعه موردی شهر تهران به دلیل پر جمعیت ترین شهر ایران انتخاب شده است. شبکه فعلی BSC تهران از 22 منطقه اهدا تشکیل شده است که با توجه به مختصات جغرافیایی و میانگین خون به دست آمده است. با توجه به جمعیت متراکم و نقش مهم آن در تأمین خون در کل کشور، هرگونه افت و از بین رفتن خون رسانی توسط شبکه BSC تهران قطعاً نه تنها شهر بلکه کل کشور را در معرض خطر کاملی قرار می دهد. در نتیجه، وجود مراکز مکمل برای مشارکت در روند تولید خون، علاوه بر مرکز خون منطقه ای موجود، برای شبکه BSC بسیار سودمند است. از روش FAHP-GRA ترکیبی برای تعیین مناسب ترین تجهیزات کمکی به عنوان SBC ها برای شرکت در فرایند تولید به کار گرفته شده است. سپس این مراحل مکان های مورد نظر کاندید با وزن های مختلفی که DM  میدهد به دست میاید.

در ادامه، سیزده رویکرد مدل سازی عدم اطمینان (جدول زیر) با به کارگیری پارامترهای مبهم تجزیه و تحلیل و مقایسه شده اند. برای این منظور، ما به طور یکنواخت 20 سناریو از پارامترهای تصادفی ایجاد  کرده ایم. میانگین انحراف استاندارد و ضریب تغییرات برای هر مدل گزارش شده است. نتایج جدول زیر، نشان می دهد که در بین این مدل ها،  HRPP-II (C)کمترین هزینه شبکه را به دست می دهد و HRPP-III (C) کمترین میانگین انحراف معیار را تحت سناریو های مختلف ارائه می دهد. در بین مدل های پیشنهادی، مدلهای  HRPP-I (c) و  HRPP-II (c) از نظر میانگین  و همچنین انحراف معیار و اندازه گیری CV در رابطه با بخش اول تابع هدف، بهتر از مدلهای دیگر هستند. با این حال، این مدل ها عملکرد ضعیفی در رابطه با بخش دوم تابع هدف دارند.

مدل HRPP-III (a)  از سایر مدل ها در مورد بخش دوم تابع هدف، بهتر است. در مقابل، عملکرد قابل قبولی در رابطه با بخش اول تابع هدف ندارد. HWRPP  و BPCCP (a) بدترین عملکرد را در مورد بخش اول تابع هدف و عملکرد متوسطی در رابطه با بخش دوم تابع هدف دارند. نسخه های HWRRP و BPCPP (a) برای DM های کاملاً محافظه کار و ریسک گریز توصیه می شوند در بین مدلهای ارائه شده، HWRPP و BPCCP  به جز نسخه c  دارای بدترین عملکرد در رابطه با انحراف معیار هستند. به همین دلیل است که استواری بهینگی و شدنی در تابع هدف آنها نادیده گرفته می شوند. اگر فقط تابع  هدف هزینه در نظر گرفته شود،  HRPP-I (c) از انواع دیگر HRPP عملکرد بهتری دارد. اگر DM فقط نسبت به انحراف تابع هدف از  مقدار بهینه مورد انتظار حساس باشد HRPP-II (c) بهترین عملکرد را در بین نسخه های مختلف مدل HRPP-II دارد، بنابراین استفاده از HRPP-II (c) برای مطالعه موردی تحقیق پیشنهاد می شود.