طراحی شبکه زنجیره تامین خون قابل‌اطمینان با اختلال در تسهیلات: یک کاربرد در دنیای واقعی (مقاله دوم)

چکیده:

خونرسانی بیمارستانها در بلایا یک مسئله مهم در مدیریت زنجیره تأمین است. در این مقاله، یک مدل مکانیابی-تخصیص استوار پویا برای طراحی شبکه زنجیره تامین خون تحت ریسک‌های ناشی از اختلال و عدم‌قطعیت ارائه شده است.  یک رویکرد استوار مبتنی بر سناریو برای حل و فصل عدم‌قطعیت مسئله (مانند تغییرات دوره‌ای تقاضاها و اختلالات تسهیلات) با مدل سازگار شده است. در نظر گرفته می‌شود که تأثیر اختلال بر تسهیلات به میزان سرمایه‌گذاری اولیه برای افتتاح آن‌ها بستگی دارد (که تحت تأثیر بودجه تخصیص یافته قرار می‌گیرند). این مدل با استفاده از یک نمونه واقعی اعتبارسنجی شده. تقاضا و اختلال به عنوان پارامترهای عدم‌قطعیت در نظر گرفته است. برای مسائل در مقیاس بزرگ، دو الگوریتم فراابتکاری، یعنی الگوریتم رقابتی استعماری خود سازگار(SAICA (و الگوریتم علف‌های هرز (IWO) برای حل مدل ارائه شده‌اند. علاوه ‌بر این، چندین نمونه عددی از بینش‌های مدیریتی ارزیابی می‌شود.

کلید واژه‌ها: لجستیک، شبکه زنجیره تامین خون، مکانیابی-تخصیص، ریسک اختلال و بحران، بهینه‌سازی استوار و آنالیز عملکرد

مقدمه:

 خون یک کالای معمولی نیست زیرا تقاضای آن نسبتاً تصادفی و خون انسان منبع نادر و حیاتی است که فقط توسط انسان تامین می‌شود و از آنجایی که در حال حاضر کالای دیگری وجود ندارد که بتواند خون تامین کند و همچنین تقاضای آن نسبتا تصادفی است بنابراین حفظ سطح عرضه برای تحقق تقاضا بسیار مهم است .

در یک زنجیره تامین، حادثه زمانی‌ست که یک یا چند فعالیت زنجیره تامین غیرفعال و تسهیلات مختل ‌شوند.

دو نوع ریسک را می‌توان از نظر زنجیره تأمین تعریف کرد ریسک‌های عملیاتی و خرابی. ریسک عملیاتی در اثر اختلالات درونی زنجیره (به عنوان مثال ، تقاضای نامشخص، ظرفیت نامشخص و هزینه های نامشخص زنجیره) ایجاد می‌شود در حالی که ریسک خرابی در اثر حوادث طبیعی یا غیرطبیعی (به عنوان مثال زلزله، سیل، حملات تروریستی و آتش سوزی) ایجاد می‌شود. در بیشتر موارد، ریسک خرابی تاثیر بیشتری از ریسک عملیاتی برعملکرد زنجیره تامین دارد. برنامه‌ریزی بهینه‌سازی استوار، رویکردی ریسک‌گریز برای مقابله با عدم‌قطعیت است.

این مقاله یک شبکه با مدل استوار جدید، با در نظر گرفتن ریسک اختلال و عدم‌قطعیت تقاضا در شرایط بحران و همچنین با پیاده‌سازی در یک مطالعه موردی واقعی، طراحی شدده‌است.

خلاصه مرور ادبیات:

تأثیرات یک بحران بر تسهیلات (مثلاً اختلال و محدودیت بودجه) یکی از مهمترین موضوعات در اکثر کشورها است که به صورت مدیریتی مورد توجه قرار نگرفته است. علاوه ‌بر این، دانستن تعداد تسهیلات مورد نیاز در سیستم‌های اضطراری یکی از موضوعات قابل چالش در بین مدیران است که باید توجه بیشتری به آن شود. بهتر است که این مدل در شرایط واقعی تولید شود تا کاربردی‌تر باشد.  

برای غلبه بر این کاستی‌ها و پر‌کردن این شکاف‌ها، یک شبکه طراحی استوار زنجیره تأمین خون تحت عدم‌قطعیت تقاضا و اختلال، برای بررسی بهترین حل‌ها در دنیای واقعی و در مقیاس بزرگ، توسعه داده است.

در این مقاله، برخی از شکاف‌ها در حوزه زنجیره تامین خون پوشانده شده، که شامل:

         ·            در نظر گرفتن هر دو نوع ریسک، که تاکنون در ادبیات زنجیره تامین خون پس از فاجعه مورد توجه قرار نگرفته است.
         ·            در نظر گرفتن دو نوع تسهیلات قابل اطمینان و غیرقابل اطمینان و تأثیر اختلال بر این تسهیلات.
         ·            پیشنهاد یک مدل جدید و کاربردی در زنجیره تامین خون عدم قطعیت.
         ·            حل این مدل در یک مطالعه موردی در دنیای واقعی، که در یک مورد اضطراری از کمبود خون رنج می‌برد.
         ·            فرض مدل چند دوره‌ای در شرایط پس از حادثه.  اکثر مطالعات در این زمینه، مدل‌ها را به صورت تک دوره‌ای در نظر می‌گیرند، در حالی که پس از حادثه، به                دلیل ماهیت عدم‌قطعیت، تقاضا را باید در دوره‌های مختلف در نظر گرفت.
         ·            در نظر گرفتن بودجه موجود برای مدل.  به گفته کارشناسان، یکی از مهمترین موضوعات برای مراکز خون، بودجه در نظر گرفته شده توسط دولت و استفاده                  بهینه از آن در مراکز و تسهیلات است.
         ·            بررسی عدم‌قطعیت در برخی از پارامترهای مسئله مانند تقاضا و اختلال در تسهیلات سیار.
         ·            در نظر گرفتن مفهوم استوار برای مقابله با عدم‌قطعیت.
         ·            استفاده از الگوریتم رقابت استعماری خود سازگار )SAICA(برای حل مدل و مقایسه آن با الگوریتم بهینه سازی علف‌های هرز )IWO( 

علاوه‌بر این، برای کارآیی این موضوع، یک مطالعه موردی در استان مازندران واقع در شمال ایران در نظر گرفته شده است که درگیر زلزله‌زدگی و سیلاب است و بیش از سایر استان‌ها از کمبود خون رنج می‌برند.

تعریف مسئله و مدل پیشنهادی:

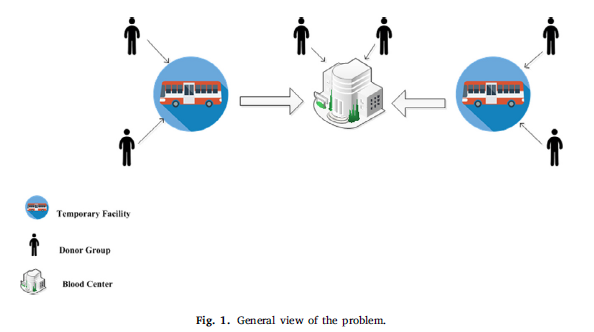
تخصیص تسهیلات سیار به مراکز، اهداکنندگان به تسهیلات سیار و مرکز و جابجایی‌خون بین گره‌ها در شکل 1 نشان داده شده است. محتوای این مقاله شامل مکانیابی تسهیلات سیار و مراکز خونی در شبکه زنجیره تامین خون و تخصیص تسهیلات و اهداکنندگان در وضعیت حادثه است. لازم به ذکر است در صورت بروز حادثه، تسهیلات دچار اختلال می‌شوند که در این صورت میزان اختلال در هر تسهیل و مرکز به سرمایه‌گذاری اولیه برای ساخت آن بستگی دارد. همچنین، این حادثه بر تقاضای خون مورد نیاز بیمارستان‌ها تأثیر خواهد گذاشت.

مدل پیشنهادی در شرایط قطعی و روباست حل می‌شود. دلیل انتخاب این مبحث، خاصیت حیاتی ماده خونی و این واقعیت، که کشورها همیشه به‌ویژه در زمان حادثه با کمبود خون روبرو هستند، می‌باشد. یک مدل فرموله‌شده استوار با توجه به عدم‌قطعیت برخی پارامترها از جمله تقاضا و اختلال ارائه شده است.

برنامه‌ریزی بهینه ‌سازی استوار، یک روش برای بررسی به عدم قطعیت در مسائل مکانیابی است. فرمول نهایی مدل بهینه سازی استوار :

                           

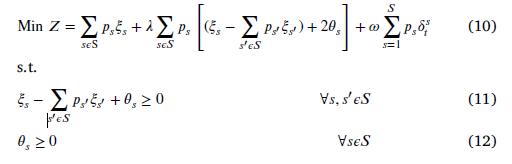
فرضیات این مدل به شرح زیر است:

         ·            در این مدل دو نوع تسهیلات در نظر گرفته شده است تسهیلات سیار و مراکز خون.  اختلالات در تسهیلات سیار اتفاق می‌افتد و مطابق مطالعه موردی، مراکز خون در برابر اختلالات در امان هستند.  بنابراین، تسهیلات سیار و مراکز خونی به ترتیب تسهیلاتی غیرقابل اطمینان و قابل اطمینان در نظر گرفته می‌شوند.

         ·            هزینه ساخت مرکز خون بسیار بیشتر از یک تسهیل سیار است.

         ·            هر اهدا‌کننده می‌تواند به مراکز خون یا تسهیلات سیار مراجعه کند.

         ·            احتمال اختلال در تسهیلات سیار به مقدار سرمایه گذاری اولیه برای افتتاح آنها بستگی دارد به این معنی که افزایش سرمایه گذاری باعث کاهش اثرات اختلال  است.  به عنوان مثال، در مراکز خونی به دلیل سرمایه‌گذاری زیاد، این مراکز دچار اختلال  نمی‌شود.

         ·            بودجه برنامه ریزی شده روی این مسئله و پاسخ گویی تقاضا تأثیر دارد.

         ·            حادثه بر تقاضای خون بیمارستان‌ها تأثیر می گذارد.

         ·            فرض بر این است که هنگام ایجاد اختلال در یک تسهیل، تسهیل به طور کامل خراب نمی‌شود.  بلکه تسهیلات فقط بخشی از ظرفیت خدمات‌رسانی در شرایط اختلال از دست می‌دهند.

         ·            برای کنترل بهتر تصمیمات میان‌مدت و نوسانات دوره‌ای تقاضا، مدل چند دوره‌ای در نظر گرفته شده است.

هدف از مدل ارائه شده ، تصمیم گیری بهینه در مورد:

         ·            مکانیابی مراکز خون

         ·            مکانیابی و انتقال تسهیلات سیار

         ·            تخصیص اهداکنندگان به مراکز خون یا تسهیلات سیار واقع در منطقه پوشش

         ·            تعداد تسهیلات سیار موجود برای جمع آوری و انتقال خون به مراکز در هر دوره زمانی و تحت هر سناریو. 

فرموله کردن مدل:

حداقل سازی تابع هدف هزینه در معاده‌های 13 تا 16 محاسبه شده است:

معادله13، هزینه ثابت احداث تسهیلات

معادله14، هزینه عملیاتی شامل هزینه جمع آوری خون اهداکنندگان

معادله15، هزینه حمل‌و‌نقل شامل هزینه انتقال تسهیلات سیار به مکان‌های دیگر و هزینه انتقال خون جمع‌آوری شده به مرکز خون

معادله17،  هزینه از دست دادن خون، شامل هزینه از دست دادن ظرفیت تسهیلات سیار در صورت بروز اختلال

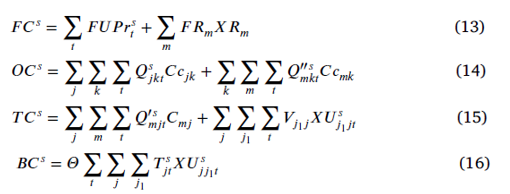
تابع هدف با استفاده از روش مدل استوار به شرح زیر فرموله شده است:

  

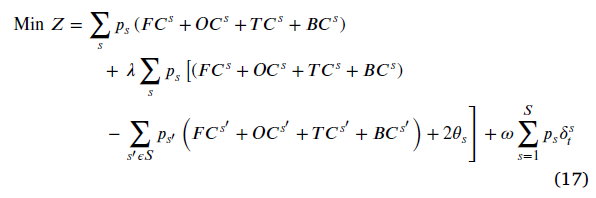
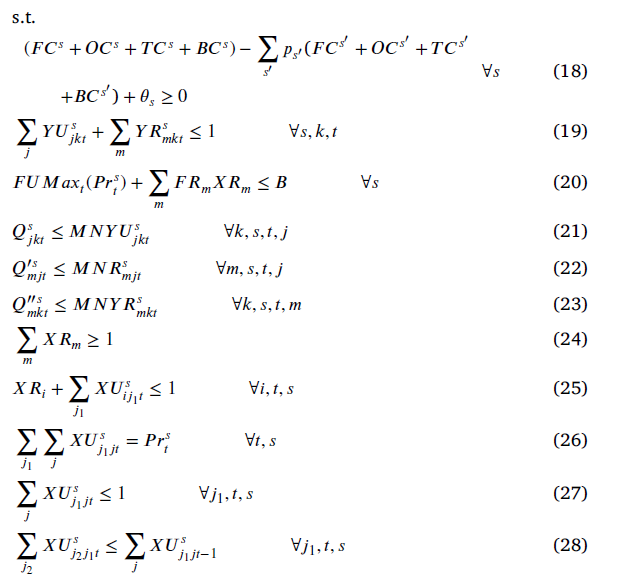
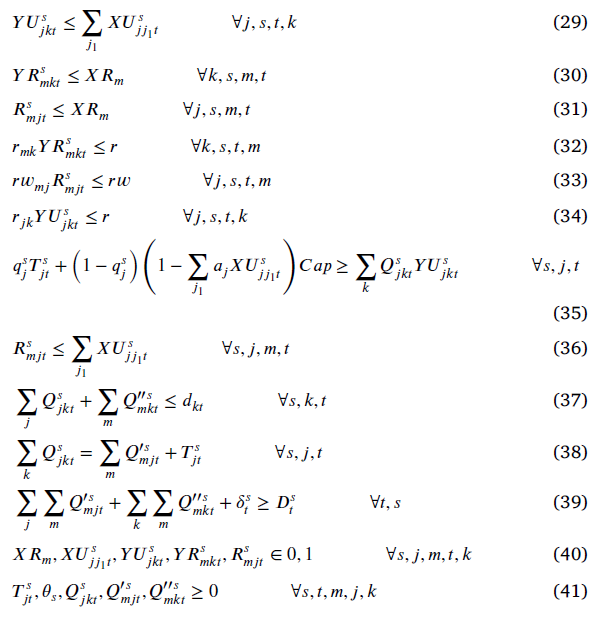
محدودیت (18) معادله کمکی استوار است.

محدودیت (19) نشان می‌دهد که فقط یک مرکز خون یا یک مرکز سیار می‌تواند خون از اهدا‌کنندگان دریافت کند (نه هر دوی آنها)

محدودیت (20) بودجه ساخت تسهیلات را نشان می‌دهد.

محدودیت‌های (21)-(22) تضمین می‌کند در صورت تخصیص اهداکنندگان به مراکز یا تسهیلات سیار، واحدهای خونی به مرکز خون انتقال داده شوند.

محدودیت (24) تضمین می‌کند که حداقل باید یک مرکز خون احداث شود زیرا تسهیلات سیار باید واحدهای خونی را به این مرکز تحویل دهند و این مرکز مسئولیت آزمایش و جمع آوری واحدهای خونی برای مصارف بیمارستان را برعهده دارد.

محدودیت (25) تضمین می‌کند که فقط یک تسهیل سیار یا مرکز در محل i قرار بگیرد.

محدودیت (26) تعداد تسهیلات سیار مورد نیاز را نشان می‌دهد.

محدودیت (27) تصریح می‌کند که در هر دوره حداکثر یک تسهیل سیار به مکان j1 می‌تواند منتقل شود.

محدودیت (28) تضمین می‌کند که تسهیلات سیار از محلی که تسهیلات در آنجا واقع شده است می‌توانند تغییر مکان دهند.

محدودیت (29) اطمینان می‌دهد که اهداکنندگان فقط به تسهیل سیار مستقر می‌توانند خون بدهند.

محدودیت (30) تضمین می‌کند که اهداکنندگان فقط به مرکز خونی مستقر می‌توانند خون بدهند شوند

محدودیت (31) تضمین می‌کند درصورتی که مرکز خون m مستقر شود، تسهیل سیار j می‌تواند به آن اختصاص یابد.

محدودیت‌ها (32)-(34) حاکی از شعاع پوشش دهنده اهداکنندگان با مرکز خون، اهداکنندگان با تسهیلات سیار و تسهیلات سیار با مرکز خون است.

محدودیت (35) ظرفیت تسهیلات سیار را با در نظر گرفتن اختلال بیان می‌کند.

محدودیت (36) تضمین می‌کند که مرکز خون فقط به تسهیلات سیار مستقر می‌تواند اختصاص یابد.

محدودیت (37) تعداد واحدهای خونی اهدا شده در هر دوره را محدود می‌کند.

محدودیت (38) نشان می‌دهد که برخی از واحدهای خونی تسهیل سیار به یک مرکز خون منتقل می‌شوند و برخی از آن‌ها نیز به دلیل اختلال از بین می‌روند.

محدودیت (39) یک محدودیت کنترل است که نشان می‌دهد تقاضای مطلوب باید در هر دوره برآورده شود.

خطی سازی:

تابع هدف غیرخطی است. بنابراین یک متغیر جدید تعریف می‌شود و به صورت زیر باز نویسی می‌شود:

 

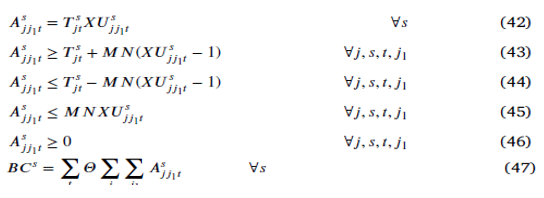
محدودیت(35) نیز  غیر خطی است و به صورت زیر آن را خطی می‌کنیم:

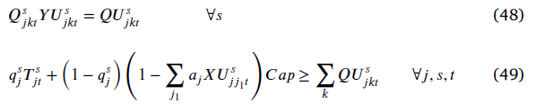
روش حل:

از آنجا که حل مسائل مکانیابی در اندازه‌های بزرگ زمان‌بر و np-hard هستند. از الگوریتم‌های جستجو فراابتکاری برای حل آن‌ها استفاده می‌شود، زیرا GAMS قادر به حل آن نیست.

در این مقاله، ما یک الگوریتم رقابتی استعماری خود سازگار(SAICA(برای حل مدل پیشنهاد می‌کنیم.

علاوه‌بر این‌، یک الگوریتم بهینه‌سازی علف‌های هرز تهاجمی(IWO( برای ارزیابی کارایی  SAICA ارائه شده است.

 الگوریتم رقابت استعماری

الگوریتم رقابتی استعماری (ICA) یک الگوریتم جستجوی جهانی با انگیزه سیاسی برای حل بسیاری از مسائل بهینه‌سازی است. مانند الگوریتم ژنتیک، که با یک جمعیت اولیه به نام کروموزوم آغاز می شود، ICA  با جمعیت مبتدی به نام کشور شروع می‌شود. سپس براساس هزینه آن‌ها، برخی از آن‌ها با هزینه پایین‌تر (بهترین حل‌ها در جمعیت) به عنوان استعمارگر انتخاب می‌شوند و سایر حل‌های با هزینه بیشتر بر اساس قدرت خود به استعمارگران اختصاص می یابند.  بنابراین، امپراتوری‌های اولیه توسط استعمارگران و مستعمراتشان ایجاد می‌شوند. پس از آن، مانند سیاست جذب، مستعمرات شروع به جابجایی به سمت استعمارگران وابسته به‌خود می‌کنند.  سپس، رقابت بین همه امپراتوری‌ها آغاز می‌شود. کل قدرت یک امپراتوری توسط دو عامل تعیین می‌شود که یکی از آن‌ها قدرت استعمارگران و دیگری قدرت مستعمراتشان است. یک امپراطوری اگر نتواند قدرت خود را افزایش دهد، از بین می‌رود.  بنابراین، امپراتوری‌های بازنده از بین می‌روند و در نهایت فقط یک امپراتوری باقی می‌ماند.

1.      تولید امپراتوری‌های اولیه:

در ICA، یک کشور به عنوان آرایه‌ای برای حل یک مسئله بهینه‌سازی n بعدی، در زیر تشکیل شده است:

برای شروع این الگوریتم، Npop  به عنوان جمعیت اولیه ایجاد می‌شود و سپس استعمارگران به عنوان Nimp  که تعدادی از قدرتمندترین کشورها هستند، درنظر گرفته می‌شود. در این الگوریتم، دو نوع کشور وجود دارد که عبارتند از استعمارگر و مستعمره. مستعمرات بر اساس قدرتشان بین استعمارگران توزیع می شوند، بنابراین هزینه نرمالیز شده یک استعمارگر:

 

مستعمرات متناسب با قدرت استعمارگران بین آن‌ها تقسیم می‌شوند، بنابراین احتمال تملک هر استعمارگر به شرح زیر است:

                       

 لازم به ذکر است که در این مطالعه از تابع نمایی برای این احتمال استفاده شده است

2.      قدرت یک امپراتوری:

قدرت کل یک امپراتوری معادل قدرت استعمارگر و درصد متوسط ​​قدرت مستعمرات آن است که به شرح زیر است:

  

3.      جذب:

عملگر جذب در شکل 3 نشان داده شده است.

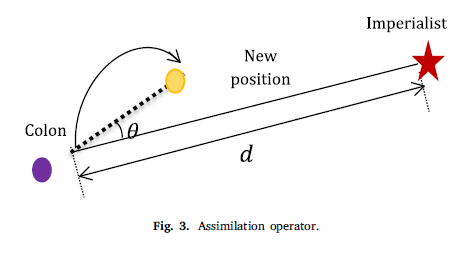
مستعمرات با در نظر گرفتن یک انحراف تصادفی، به سمت استعمارگران حرکت می‌کنند.  یک عدد تصادفی است که از توزیع یکنواخت پیروی می‌کند. همچنین d به عنوان فاصله بین استعمارگران و مستعمره در نظر گرفته می شود.

4.      متقاطع

در این مرحله، اطلاعات مستعمرات با استفاده از عملگرهای متقاطع  p-Crossover  بین خودشان به اشتراک گذاشته می‌شود.

5.      انقلاب

بروز انقلاب تغییرات ناگهانی را در ویژگی‌های اجتماعی و سیاسی یک کشور ایجاد می‌کند. در الگوریتم رقابت استعماری، انقلاب با جابجایی تصادفی یک کشور مستعمره به یک موقعیت تصادفی جدید مدلسازی می‌شود.

همچنین انقلاب خطر ابتلا به دام در جستجوهای محلی را کاهش می دهد.

6.      تبادل موقعیت

اگر مستعمره قوی‌تر از استعمارگر باشد، موقعیت مستعمره و استعمارگر ممکن است تغییر کند.

7.      از بین بردن امپراتوری‌های بی‌قدرت

در طی روند رقابت، امپراتوری‌های ضعیف از بین می‌روند

8.      معیارهای توقف

الگوریتم پیشنهادی با برقراری حداکثر تکرار یا باقی ماندن یک امپراتوری در مرحله پردازش، متوقف می‌شود.

ICA خود سازگار

در ICA، برخی از مستعمرات تحت تأثیر امپراطوری کشورهای دیگر قرار دارند یا ممکن است امپراطوری‌ها داده‌های متقابل را با یکدیگر تبادل کنند. عملگر متقاطع یک عامل کاربردی برای این مفهوم است. در روش حل پیشنهادی استفاده از بیشتر عملگرهای تقاطع بدون افزایش زمان حل امکان پذیر است. برای این کار، عملگرهای مختلفی را ادغام می‌کنیم. به همین دلیل، الگوریتم پیشنهادی برای حل SAICA (الگوریتم رقابت استعماری خود سازگار) نامیده می‌شود.

مقدار تابع هدف به عنوان OFV در این مقاله نشان داده شده است.

نتایج تجربی

برای اعتبار سنجی مدل پیشنهادی، با استفاده از داده‌های اخذ شده از یکی از شهرهای اصلی استان مازندران واقع در شمال ایران، مسئله حل شده است.

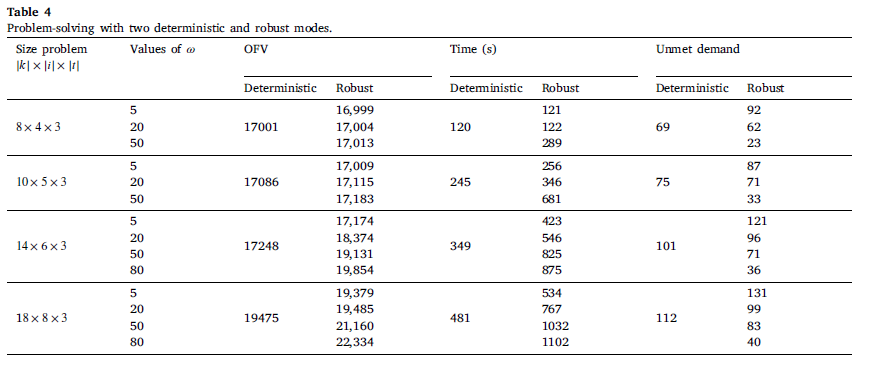
جدول 4 ، مقایسه بین روش‌های قطعی (حل شده با GAMS)  و استوار را برای مسائل کوچک و متوسط ​​نشان می‌دهد. مقادیر تابع هدف با رویکرد استوار به مقدار ω بستگی دارد. به عنوان مثال، برای ω بالاتر مدل، بیشترین مقدار تقاضا را برآورده می‌سازد. درنتیجه، تابع هدف و زمان حل افزایش می‌یابد. علاوه‌بر این، برای مقادیر بالایω ، مدل در نظر دارد که تقریباً تمام سناریوها را امکان‌پذیر سازد. به همین دلیل میزان تابع هدف نسبت به نمونه‌های قطعی بیشتر است.

                       

ارزیابی عملکرد مدل:

در این مقاله ، مقدار تقاضای برآورده نشده در شرایط استوار و قطعی مقایسه می شود.

در جدول، زمان حل و تقاضای برآورده نشده در مدل استوار بهتر از مدل قطعی است. مثلا حل استوار با مقدار ω  برابر80،  تنها با صرف 14٪ هزینه بیشتر، تقاضای برآورده نشده را در مقایسه با حل قطعی (مقدار زیادی) کاهش می‌دهد. می‌توان نتیجه گرفت که مدل ارائه شده عملکرد بهتری نشان می‌دهد زیرا عدم قطعیت پارامترها را نادیده نمی‌گیرد.

مثال عددی

حل های IWO و SAICA در مسائل کوچک و بزرگ مقایسه می شوند.

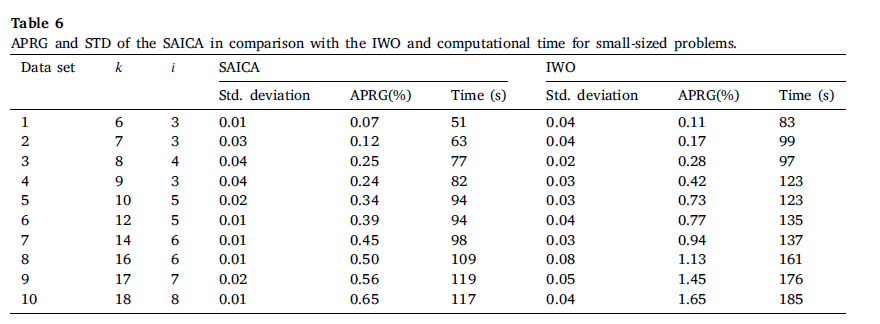
در جدول 6، برای ارزیابی اختلاف بین هر الگوریتم با حل دقیق (حل شده توسط  GAMS)، میانگین درصد اختلاف نسبی )APRG(محاسبه می‌شود. APRG برای هر دو الگوریتم کمتر از 2 درصد است.. بنابراین، هر دو الگوریتم حل‌های  معقول منجر می‌شوند.

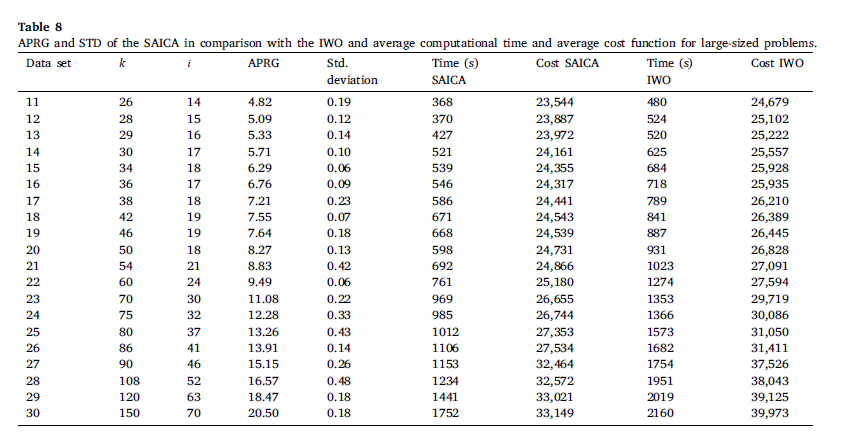
در جدول 8، میانگین اختلاف درصد، انحراف استاندارد و زمان حل هردو الگوریتم فراابتکاری را محاسبه کرده است. زمان محاسبه الگوریتم‌های فراابتکاری با افزایش اندازه مسائل افزایش می‌یابد. این نتایج نشان می‌دهد که رویکردهای هر دو روش فراابتکاری می‌توانند در یک زمان معقول، حل‌های تقریباً بهینه را پیدا کنند.در حالی که SAICA  در همه‌ی مسائل از نظر CPU و APRG بهتر از IWO است.

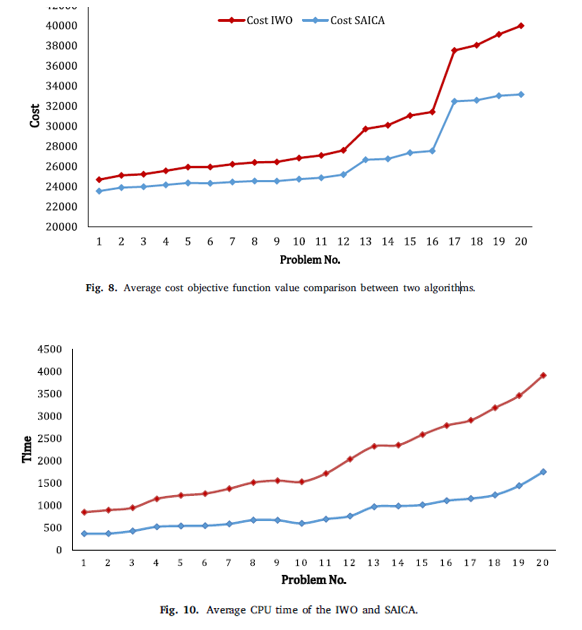
شکل 8، مقایسه بین دو الگوریتم از نظر مقدار تابع هدف هزینه را نشان می‌دهد، که در کلیه مجموعه‌ها هزینه SAICAکمتر از IWO است.

شکل 10، نشان می‌دهد با افزایش تعداد مسائل، زمان حل IWO بیشتر از SAICA می‌شود. در نتیجه، عملکرد SAICA در هر دو مسئله کوچک و بزرگ بهتر از IWO است.

 

مطالعه موردی

سازمان انتقال خون ایران )IBTO(یکی از مهمترین مؤسسات ایران است که وظیفه اصلی آن تأمین خون بویژه در حوادث و فوریت‌های پزشکی است.

یکی از مهمترین زیر مجموعه‌های این موسسه، سازمان انتقال استان مازندران است.

این استان در شمال ایران یک استان بزرگ است و از نظر حوادث طبیعی با جمعیت بیش از سه میلیون یکی از استان های خطرناک است. مدل ارائه شده با هدف توسعه طراحی شبکه زنجیره تامین خون کارآمد در مازندران انجام شده است. اطلاعات جمع آوری شده از 73 شهر و 150 روستای اطراف واقع در مازندران است. هزینه انتقال تسهیلات سیار متناسب با فواصل بین آن‌ها در نظر گرفته می‌شود. این استان در معرض برخی بلایای خطرناک (به عنوان مثال ، زلزله و سیل) قرار گرفته است.

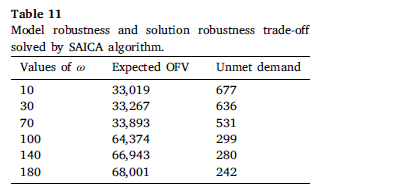
در جدول 11 ، افزایش پارامتر امگا منجر به تاسیس تسهیلات بیشتر برای پوشش تقاضا می‌شود، بنابراین با افزایش امگا، مقدار میانگین تابع هدف افزایش می‌یابد و تقاضای برآورده نشده کاهش می‌یابد.

       

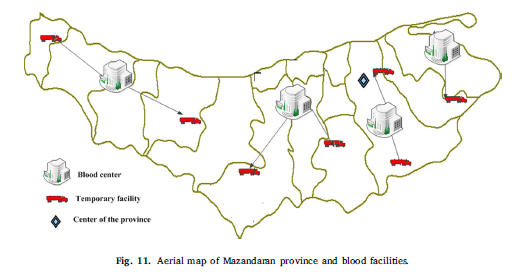
شکل 11 مکان‌های کاندید مراکز خونی و تسهیلات سیار را برای یکی از دوره ها نشان می‌دهد همانطور که در شکل دیده می‌شود چهار مرکز در چهار شهر تاسیس شده و هفت تسهیل سیار برای جمع‌آوری خون آن‌ها تخصیص داده شده است.

            

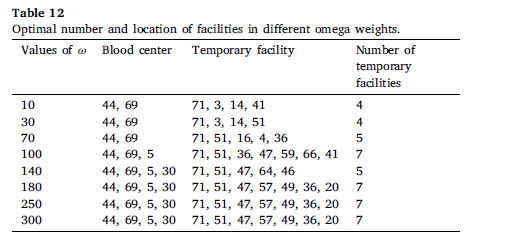
براساس اطلاعات جدول 12 ، افزایش امگا مدل را مجبور می‌کند که مقدار تقاضای برآورده نشده را کاهش دهد و در نتیجه ، تعداد مراکز و تسهیلات سیار افزایش یابد. در این جدول مکان 44 و 69 مکان‌های بهینه برای همه‌ی مقادیر امگا هستند. به عبارت دیگر، این دو مکان، مکان مناسبی برای تجهیزات مراکز خونی با بودجه‌های متنوع هستند.  وقتی سیستم با کمبود بودجه مواجه ‌است، این دو مکان بهترین حل برای کاهش کل هزینه و تحقق بیشترین تقاضا است. بنابراین، باید روی این دو مکان سرمایه‌گذاری کرد.

              

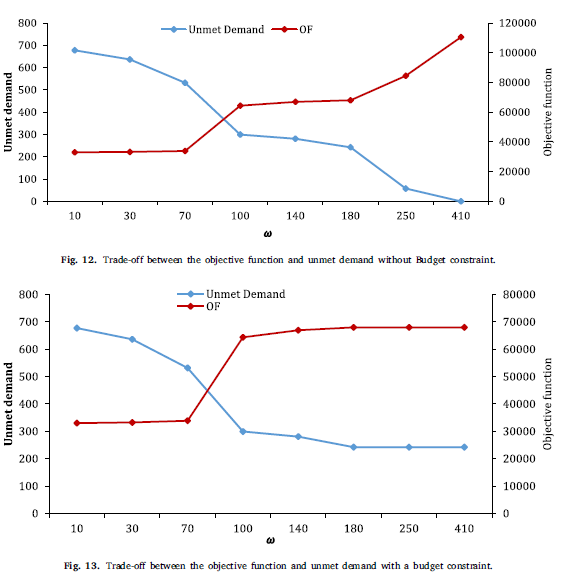
شکل 12، حساسیت مقادیر تابع هدف و تقاضای برآورده نشده برای مقادیر مختلف امگا را نشان می‌دهد. که  با افزایش پارامتر امگا به 180، تقاضای بیشتری با احداث امکانات بیشتر ،با افزایش هزینه کل پوشانده شود.

برای نشان دادن تأثیر محدودیت بودجه، مدل با محدودیت و بدون محدودیت بودجه حل شده و نتایج در شکل 12 و 13 نشان داده شده است. بر اساس این ارقام، بدون محدودیت بودجه، امگا 410 و هزینه 11.0456، تقاضای برآورده نشده را به صفر می‌رسد ، بدین معنی که اگر تصمیم گیرندگان بخواهند کل تقاضا پاسخ بدهند، باید 11.0456 هزینه کنند اما، با در نظر گرفتن محدودیت بودجه، بهترین تصمیم این است که مقدار تقاضای برآورده نشده(که زیاد نیست)، را بپذیرند.

  

بینش مدیریتی

برخی از مهمترین بینش های ارائه شده در این مقاله شامل:

         ·            اتخاذ بهترین تصمیم در یک سیستم بهداشت و درمان و با یک منبع فاسد شدنی.

         ·            قابله با عدم قطعیت در مواقع اضطراری.

         ·            مقابله با هر دو ریسک عملیاتی و خرابی در شبکه.

         ·            اتخاذ بهترین تصمیم برای ارزیابی سطح بودجه در شبکه.

         ·            اتخاذ بهترین تصمیم برای تجهیزات مراکز و مکانیابی تسهیلات در شبکه در یک مطالعه موردی واقعی.

نتیجه

در این مقاله به دلیل توجه بیشتر به بخش مراقبت‌های بهداشتی به ویژه در مواقع اضطراری، به بررسی تسهیلات در شبکه زنجیره تامین خون پرداخته شده است. یک مدل ریاضی جدید برای تصمیم‌گیری‌های مؤثر درمورد مکانیابی_تخصیص شبکه زنجیره تامین خون در دوره‌های پس از حادثه، با در نظر گرفتن محدودیت بودجه برای ساخت تسهیلات و مراکز خونی، ارائه کرده‌ایم. همچنین ریسک اختلال و تأثیرات آن برای هر تسهیلات سیار در نظر گرفته شده است. با توجه به وجود شرایط حادثه، ما این مدل را تحت عدم قطعیت توسعه داده‌ایم و یک مدل بهینه‌سازی روباست را ارائه کردیم. یک مطالعه موردی واقعی برای ارزیابی مدل ارائه شده است. با توجه به دشواری مسائل مکانیابی_تخصیص تسهیلات، الگوریتم رقابت استعماری خودسازگار(SAICA(برای حل مدل پیشنهادی در نظر گرفته شده است. علاوه‌بر این، برای ارزیابی کارایی این الگوریتم، عملکرد آن با الگوریتم بهینه‌سازی علف‌های هرز(IWO(مقایسه شده است. سرانجام، برای ارائه برخی از دیدگاه‌های مدیریتی برای مسئله فوق، تجزیه‌وتحلیل حساسیت برروی پارامترهای کلیدی مسئله انجام شده است.