طراحی شبکه زنجیره تامین خون اضطراری دو هدفه در زلزله با توجه به شدت زلزله (مقاله پنجم)

چکیده

این تحقیق یک مدل ریاضی چند هدفه جدید برای طراحی شبکه زنجیره تأمین خون کارآمد و مؤثر در زمین لرزه ارائه می‌دهد. برای اولین بار تأثیر شعاع تخریب زلزله در شبکه زنجیره تأمین خون در نظر گرفته شده است. دو وسیله حمل‌و‌نقل متفاوت و با سرعت و ظرفیت متغیر، برای انتقال خون از مراکز جمع‌آوری خون به مراکز خون استفاده می‌شود. با این حال، تعداد وسیله‌های حمل‌و‌نقل موجود در هر محل محدود است. برای حل مدل برنامه‌ریزی عدد صحیح خطی چند هدفه پیشنهادی، از پنج روش تصمیم‌گیری چند هدفه و همچنین روش lexicographic weighted Tchebycheff استفاده شده است تا حل‌های بهینه پارتو را به تصمیم‌گیرنده ارائه دهد. کاربرد مدل پیشنهادی در یک مطالعه موردی در دنیای واقعی با استفاده از داده‌های آخرین زلزله در یکی از گسل‌های تهران مورد بررسی قرار گرفته‌است. با استفاده از روش‌های حل مختلف، حل‌های متفاوت بهینه پارتو برای مطالعه موردی بدست می‌آید.

کلید واژه‌ها: طراحی شبکه زنجیره تامین،  تصمیم‌گیری‌های چند هدفه،  مکانیابی و تخصیص، بهینه‌سازی چند هدفه و روش lexicographic weighted Tchebycheff

 

مقدمه

بلایای طبیعی مانند زلزله، آتشفشان، سونامی و طوفان بر زندگی انسان تأثیر می‌گذارد. در میان این‌ها، زمین لرزه رایج‌ترین و مخرب‌ترین است. در قرن گذشته‌، زمین لرزه‌ها خسارات بسیاری از جمله تخریب ساختمان‌ها و جاده‌ها و مرگ‌ومیر انسان‌ها را در جهان به وجود آورده است. بسیاری از سازمان‌ها از جمله خدمات انتقال خون و سازمان‌های غیر‌دولتی بشردوستانه (سازمان‌های مردم نهاد) نقش برجسته‌ای در مواقع اضطراری مانند بلایای طبیعی دارند. با توجه به اهمیت عملیات بشردوستانه در حین و بعد از فاجعه، بسیاری از محققان قصد داشتند مدل‌ها و دستورالعمل‌های قابل اجرا را تهیه کنند.

یکی از چالش‌های اصلی خدمات انتقال خون، مدیریت زنجیره تأمین خون به طور موثر در حین و بعد از زلزله است. زلزله شدید می‌تواند منجر به افزایش ناگهانی در تقاضای خون شود. بنابراین، طراحی زنجیره تأمین خون کارآمد در شرایط اضطراری از اهمیت زیادی برخوردار است.

در 26 دسامبر ۲۰۰۳، یک زلزله ۶.۶ ریشتر شهر بم در جنوب شرقی ایران را ویران کرد که در آن ۲۶,۲۷۱ نفر کشته و ۳۰,۰۰۰ مجروح شدند . همچنین اثر تخریب زلزله در مدل برای طراحی یک زنجیره تأمین خون قوی و مقاوم در طول زلزله در نظر گرفته شده است. از آنجا که تعداد مجروحان بسیار زیاد بود، بیمارستان‌ها خواستار فوریت‌های تامین خون شدند. متأسفانه، به دلیل زنجیره تأثیر ناکارآمد خون، از 108،000 واحد خون اهدا شده، فقط 21،000 واحد (تقریباً 23٪) به بیمارستان‌ها رسیدند. در چهار روز اول پس از زلزله، تنها 1231 (1.3٪) از واحدهای خونی اهدا شده به منطقه حادثه رسیدند. تجربیاتی از جمله حادثه بم، اهمیت یک سیستم حمل‌و‌نقل کارآمد در زنجیره تامین خون را در حین و بعد از یک بحران شدید طبیعی نشان داد. بنابراین برای پر‌کردن این خلاء به یک مدل ریاضی جدید نیاز است. برای این منظور  یک فرمول ریاضی جدید دو هدفه برای طراحی یک زنجیره تأمین خون کارآمد در حین و بعد از زلزله پیشنهاد شده است. مدل ریاضی دو هدفه پیشنهادی، زنجیره تامین خون سه‌سطحی را در نظر می‌گیرد که از گروه‌های اهداکننده، امکانات جمع‌آوری خون و مراکز خون تشکیل شده است.

هدف مدل ریاضی پاسخگویی به تصمیمات مربوط به تعیین محل احداث تسهیلات جمع‌آوری خون دائمی و سیار، تخصیص گروه‌های اهداکننده به مراکز جمع‌آوری خون، تعداد بهینه تسهیلات جمع آوری سیار و دائم خون، سطح موجودی خون در هر مرکز خون  و تعداد بهینه وسایل نقلیه و بالگردهای مورد نیاز در هر مرکز جمع‌آوری خون برای انتقال خون جمع‌آوری شده به مراکز خونی.

دو تابع هدف در نظر گرفته شده است که هدف اول آن به حداقل رساندن کل هزینه‌های زنجیره تامین خون و کل زمان حمل‌و‌نقل است. همچنین اثر تخریب زلزله در مدل در نظر گرفته شده است تا یک زنجیره تأمین خون استوار در هنگام زلزله طراحی کند.

خلاصه مرور ادبیات

برای اولین بار در این حوزه دانش، شعاع تخریب زلزله در این تحقیق در نظر گرفته شده است در حالی که مراکز جمع‌آوری خون دائم می‌توانند در اثر زلزله نابود شوند.

مورد مهم دیگر خون‌رسانی در هنگام بروز بلایا، نحوه انتقال خون جمع‌آوری شده به مناطق زلزله زده است. در این تحقیق دو وسیله حمل‌ونقل با ظرفیت محدود در نظر گرفته شده است که خون جمع‌آوری شده را به منطقه زلزله‌ زده منتقل می‌کند. علاوه بر این، تعداد محدودی از تجهیزات حمل‌ونقل موجود در هر مرکز جمع‌آوری خون وجود دارد. بنابراین، با حل مدل ریاضی چند هدفه پیشنهادی، تعداد بهینه تجهیزات حمل‌ونقل مورد نیاز تعیین می‌شود.

علاوه بر این، در کلیه تحقیقات قبلی هدف از ایجاد زنجیره تامین خون به حداقل رساندن کل هزینه‌های زنجیره تأمین است، اما در شرایط اضطراری مانند زلزله شدید، اولویت تأمین خون در اسرع وقت به دور از در نظر گرفتن هزینه‌ها است. بنابراین، این تحقیق یک تابع هدف دوم، که به حداقل رساندن کل زمان انتقال خون جمع‌آوری شده از مراکز جمع آوری خون به مراکز خون است، در نظر گرفته است.

برای حل مدل ریاضی چند هدفه، دو رویکرد بهینه‌سازی در نظر گرفته شده است. رویکرد اول روش‌های MODM و رویکرد دوم، روش lexicographic weighted Tchebycheff است که برای حل مدل چندهدفه برای یافتن حل‌های بهینه پارتو اسفاده ‌می‌شود.

حل‌های بهینه پارتو می‌تواند به تصمیم‌گیرنده کمک کند تا مناسب‌ترین حل را انتخاب کند.

تعریف مسئله

در این تحقیق، زنجیره تأمین سه سطحی از اهداکنندگان خون، مراکز جمع‌آوری خون و مراکز خون تشکیل شده است که برای طراحی شبکه زنجیره تامین خون ضروری است. دو نوع تسهیل جمع‌آوری خون که شامل تسهیلات جمع‌آوری خون دائم و سیار است وجود دارد. نمای شماتیک از زنجیره تامین خون پیشنهاد شده در شکل 1 ارائه شده است.

محل تسهیلات دائم جمع‌آوری خون ثابت است در حالی که تسهیلات سیار می‌توانند در محل‌های کاندید حرکت کنند تا خون بیشتری را از گروه‌های اهداکننده جمع کنند. خون جمع‌آوری شده در مراکز جمع‌آوری خون با استفاده از وسایل نقلیه و هلیکوپترها با هزینه، سرعت و ظرفیت ثابت و متغیر به مراکز خون منتقل می‌شود. هر دوره در جدول 2 مسئولیت هر تسهیل در زنجیره خونرسانی آورده شده است.

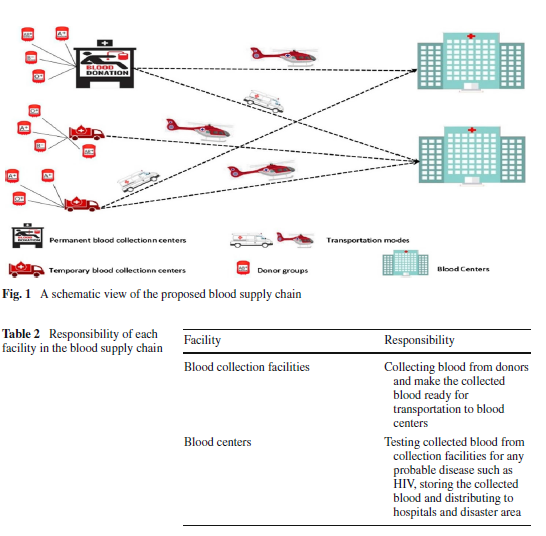
تعداد وسایل نقلیه و هلیکوپترهای انتقال خون در هر مکان و در هر دوره محدود است و با حل مدل ریاضی چند هدفه تعداد بهینه وسایل نقلیه مورد نیاز در هر محل مشخص می‌شود.

  مفروضات زیر در این تحقیق استفاده شده است:

·         حداکثر تامین خون از هر اهداکننده مشخص است.

·         تعداد تجهیزات حمل‌ونقل موجود در هر محل محدود است.

·         ظرفیت تسهیلات جمع‌آوری خون و مراکز خون محدود است

·         میزان تقاضا در  هر مرکز خون مشخص است.

با حل الگوی ریاضی چند هدفه پیشنهادی، در هر دوره تصمیمات زیر اتخاذ می شود.

·         اختصاص گروه‌های اهداکننده به مراکز جمع آوری خون.

·         جریان خون از گروه‌های اهداکننده به تسهیلات خون و مراکز خون.

·         تعداد مطلوب تسهیلات جمع‌آوری سیار و دائم خون.

·         مکانیابی بهینه تسهیلات جمع آوری خون سیار و دائمی.

·         سطح موجودی خون در هر مرکز خون در یک دوره خاص.

·         تعداد بهینه وسایل نقلیه مورد نیاز در هر مرکز جمع‌آوری خون برای انتقال خون جمع‌آوری شده به مراکز خون.

·         مقدار خون منتقل شده از هر مرکز جمع‌آوری به هر مرکز خون توسط وسایل نقلیه.

     

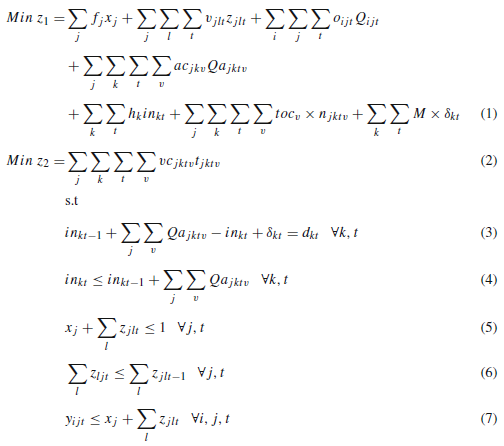
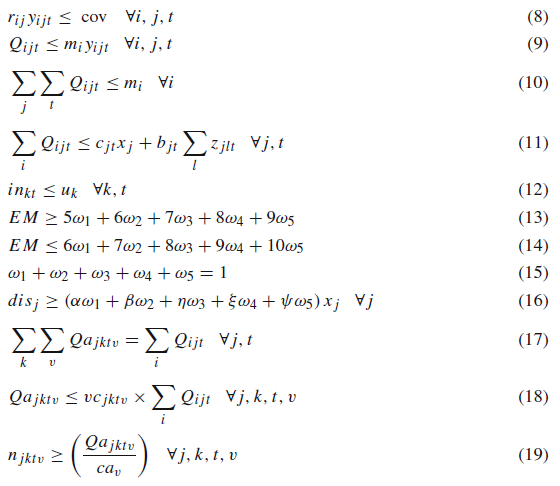
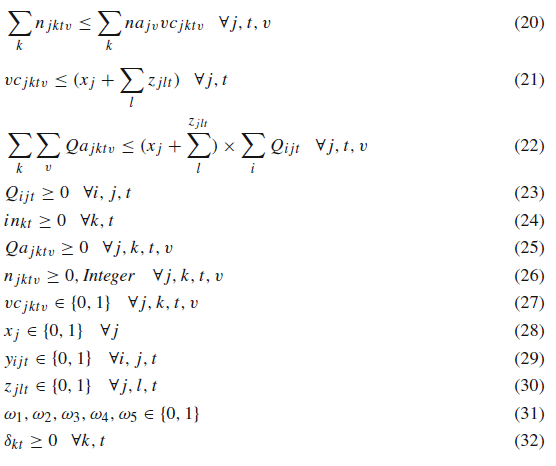
معادله 1،  هدف اول هزینه‌های زنجیره تأمین را به حداقل می‌رساند از جمله احداث مراکز جمع‌آوری خون دائم، جابجایی تسهیلات جمع‌آوری سیار خون، جمع‌آوری خون از گروه‌های اهداکننده‌، انتقال خون جمع‌آوری شده به مراکز خون، ذخیره خون در مراکز خون، هزینه ثابت وسایل حمل‌ونقل و جریمه تعیین شده برای کمبود خون.

 معادله 2، هدف دوم  به حداقل رساندن زمان حمل‌ونقل خون جمع آوری شده از مراکز جمع‌آوری خون به مراکز خون است.

محدودیت (3)  تضمین می‌کند سطح موجودی در هر مرکز خون در دوره قبلی به علاوه میزان کل خون انتقال داده شده از مراکز جمع‌آوری به آن مراکز خون، منهای موجودی در دست در مرکز خون در پایان دوره فعلی به علاوه میزان کمبود در مرکز خون فعلی، برابر با میزان کل تقاضای در مرکز خون در دوره فعلی می‌باشد. 

محدودیت (4) تضمین می‌کند که سطح موجودی دردست در دوره فعلی کمتر مساوی سطح موجودی در دست دوره قبلی به علاوه مقدار خون جمع‌آوری شده از مراکز جمع آوری منتقل شده به مرکز خون در دوره فعلی.

محدودیت (5) تضمین می کند که در هر مکان فقط یک مرکز جمع‌آوری خون قابل احداث است.

محدودیت (6) حرکت مراکز جمع‌آوری خون سیار را کنترل می‌کند.

محدودیت (7) تضمین می‌کند که هر گروه اهداکننده می‌تواند تنها به یک تسهیل جمع‌آوری خون اختصاص یابد.

محدودیت (8) نشان می‌دهد فاصله بین گروه اهداکننده و تسهیلات جمع‌آوری خون باید کوچکتر یا مساوی شعاع پوشش باشد.

محدودیت (9) تأیید می‌کند که برای جمع‌آوری خون از یک گروه اهداکننده، گروه اهداکننده باید به یک مرکز جمع‌آوری خون اختصاص یابد.

محدودیت (10) تضمین می‌کند که کل خون جمع‌آوری شده از یک گروه اهداکننده در یک مرکز جمع‌آوری خون، کمتر یا مساوی از حداکثر خونرسانی گروه‌ اهداکننده است.

محدودیت (11) محدودیت ظرفیت تسهیلات جمع‌آوری خون را نشان می‌دهد.

محدودیت (12) محدودیت ظرفیت مراکز خونی را نشان می‌دهد.

محدودیت‌ها (13)-(16) خسارات ناشی از زلزله به مراکز جمع‌آوری دائم خون را  نشان می‌دهد.

محدودیت (17) نشان می‌دهد که تسهیلات جمع‌آوری تمام خون‌های جمع آوری شده را به مراکز خون ارسال می‌کند.

محدودیت‌ها (18)-(21) تعداد وسایل نقلیه برای انتقال خون جمع‌آوری شده از مراکز جمع‌آوری خون به مراکز خون را با توجه به تعداد محدودیت وسایل حمل‌و‌نقل تعیین می‌کند.

محدودیت‌ (22) اطمینان حاصل می‌کند در صورتی که مرکز جمع‌آوری خون مستقر شود، می‌توان خون جمع‌آوری شده  را به مراکز خون منتقل کرد.

محدودیت‌های (23)-(32) مقادیر متغیرهای تصمیم‌گیری را نشان می‌دهد.

روش‌های حل

مدل ریاضی توسعه یافته در بخش قبلی یک مدل برنامه‌ریزی خطی عدد صحیح مختلط دو هدفه (MILP) است.

دو روش حل برای حل مدل‎های بهینه‌سازی چند هدفه وجود دارد:

1.      روش‌های تصمیم‌گیری چند هدفه MODM

2.      تکنیک‌های بهینه‌سازی چند هدفه

تکنیک‌های بهینه‌سازی چند هدفه مجموعه‌ای از حل‌های پارتو به نام مرزهای پارتو را ارائه می‌دهد. این حل‌های بهینه پارتو، گزینه‌های متنوعی را برای تصمیم‌گیرنده ایجاد می‌کند. اگر تعداد حل‌های پارتو زیاد باشد، انتخاب یک حل بهینه پارتو از مرزهای پارتو کار دشواری است. در این موارد، از روش‌های MODM ، که مسائل را با دیدگاه‌های مختلف مانند به حداقل رساندن انحراف هر یک از تابع هدف‌ها، حل می‌کند، قابل استفاده است. با توجه به تمام نکات فوق، هر دو تکنیک بهینه‌سازی چند هدفه و MODM  مزایای خاص خود را دارند.

روش‌های تصمیم‌گیری چند هدفه MODM

روش‌های MODM در چهار دسته طبقه‌بندی می‌شوند.

      1.            روش‌های دسته اول، بدون هیچ گونه اطلاعاتی از سوی تصمیم‌گیرنده، مسئله را حل می‌کنند، به عبارت دیگر، در این روش‌ها تصمیم‌گیرنده فقط حل به دست آمده را می‌پذیرد یا رد می‌کند.

      2.            روش‌های دسته دوم، سعی در یافتن مؤثرترین نقطه بهینه دارند که براساس اولویت‌های تعیین شده توسط تصمیم‌گیرنده، هر دو تابع هدف را به حداقل می‌رساند. بنابراین، در این دسته تصمیم‌گیرنده باید براساس اهمیت آن‌ها اولویت توابع هدف‌ را تعیین کند.

      3.            روش‌های دسته سوم به طور کلی روش‌های تعاملی نامیده می‌شوند، بدین معنی که در هر تکرار از تصمیم‌گیرنده درباره اولویت جواب‌های به دست آمده برای تعیین حل بعدی سؤال می‌شود.

      4.            در روش‌های دسته چهارم، تصمیم‌گیرنده باید در پایان، حل را براساس اولویت خود انتخاب کند.

در این مقاله از پنج روش MODM از جمله  Max-Min ، تابع مطلوبیت، دستیابی به آرمان، LP متریک و برنامه‌ریزی آرمانی برای حل مدل ریاضی دو هدفه زنجیره تامین خون استفاده شده است. 

برای ارزیابی عملکرد پنج روش MODM ، سه معیار شامل مقدار تابع هدف اول، مقدار تابع هدف دوم و زمان CPU  (زمان محاسبه) تعیین شده است.

سنجش عملکرد

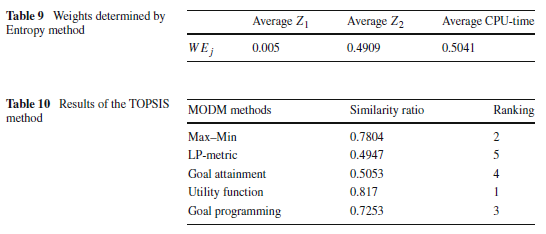
از آنجا که تعیین وزن دقیق برای هر معیار مقایسه‌ای عملا غیرممکن است، در این بخش از روش آنتروپی برای تعیین وزن  هر معیار استفاده می شود. سپس از روش TOPSIS برای نشان دادن روش برتر MODM استفاده شده است. روش آنتروپی وزن هر معیار را بدون دریافت اطلاعات از تصمیم‌گیرنده برای ماتریس تصمیم‌گیری معین، تخمین می‌زند. جدول 9 ، با استفاده از روش آنتروپی، وزن‌های بدست آمده از هر معیار را نشان می‌دهد. پس از اختصاص وزن مناسب به هر معیار، از روش )TOPSIS(برای رتبه‌بندی پنج روش MODM استفاده می‌شود. نتایج استفاده از روش TOPSIS در جدول 10 آورده شده است و روش تابع مطلوبیت بهترین روش MODM برای حل مدل توسعه یافته برنامه‌ریزی عدد صحیح خطی )MILP(است.

 

تکنیک‌های بهینه‌سازی چند هدفه

از آنجا که هر دو تابع هدف در مدل پیشنهادی چندهدفه در تضاد هستند، تدوین روشی برای ارائه حل بهینه پارتو مهم است. زیرا، در بعضی موارد تصمیم‌گیرندگان ترجیح می‌دهند از مجموعه مشخصی از حل‌های بهینه پارتو را یک جواب را انتخاب کنند.

در این مطالعه از روش lexicographic weighted Tchebycheff برای حل‌های بهینه پارتو استفاده شده است.

اجرای مدل

ایران به عنوان یکی از کشورهای مستعد زلزله در جهان است. در جدول 11 برخی از ویرانگرترین زمین لرزه‌های ثبت شده در ایران ارائه شده است. توزیع سریع و کافی خون پس از زمین لرزه‌های شدید همیشه مورد نگرانی بوده است. برای بررسی این وضعیت در یک مجموعه داده‌های واقعی برای ارزیابی اثربخشی مدل ریاضی دو هدف، اجرا می‌شود. IBTO تنها سازمانی است که مسئول کلیه فعالیت‌های مربوط به جمع‌آوری و توزیع خون است. قوانین ملی همه سازمان‌های دیگر را از هرگونه فعالیت در رابطه با انتقال خون منع کرده است. برخی از وظایف اصلی IBTO:  

(1) اصلاح استانداردهای جمع‌آوری، غربالگری، تحویل و ذخیره خون است.

(2) طراحی شبکه زنجیره تامین خون از جمله مراکز جمع‌آوری خون و مراکز توزیع.

(3)  انجام آزمایشات لازم بر روی خون اهدا شده برای اطمینان از ایمنی آن.

تهران پرجمعیت‌ترین شهر ایران، دومین شهر بزرگ در غرب آسیا و سومین شهر بزرگ در خاورمیانه با جمعیتی بالغ بر 16 میلیون نفر در منطقه وسیع کلانشهر است. تهران در 13 گسل فعال واقع شده است و آن را به یکی از محتمل‌ترین مکان‌های زلزله شدید تبدیل کرده است. این شهر به 22 منطقه شهری تقسیم شده است که هر کدام مرکز اداری خاص خود را دارند ، همانطور که در شکل 8 ارائه شده است.

برای نشان دادن اینکه توابع هدف با هم در تضاد هستند، با استفاده از داده‌های واقعی شهر تهران، هر تابع هدف به صورت جداگانه به حداقل می‌رسد و نتایج در جدول 19 نشان می‌دهد که دو تایع هدف به طور همزمان به حداقل نمی‌رسند.

جدول 20، نتایج حل مسئله با پنج روش MODM   را نشان می‌دهد. حل به دست آمده توسط پنج روش MODM از نظر مقادیر تابع هدف اول و دوم کاملاً رقابتی هستند.

جدول 21، حل‌های بهینه پارتو با استفاده از روش lexicographic weighted Tchebycheff بدست‌آمده است.

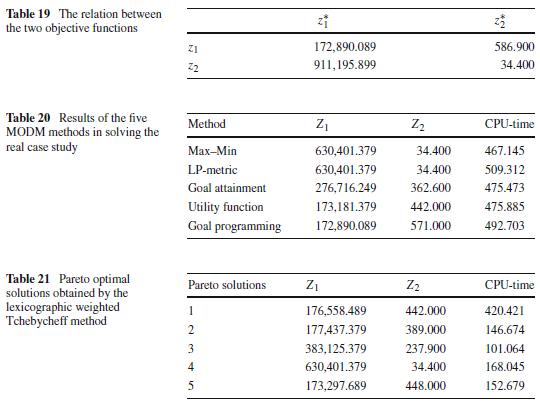
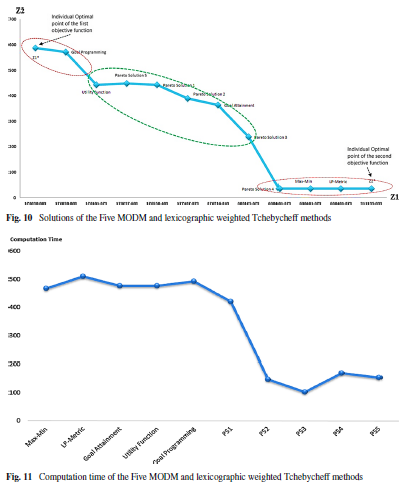
با توجه به جداول 20 و 21 نمودارهای 10 و 11 حاصل شده‌اند.

در شکل 10، مقادیر توابع هدف نمایش داده شده‌اند. حل‌های بهینه پارتو به تصمیم‌گیرنده کمک می‌کند تا مناسب‌ترین حل را انتخاب کند. به عنوان مثال، اگر اولین تابع هدف در اولویت باشد، تصمیم ‌گیرنده می‌تواند روش  Min  - Max یا LP-metric را انتخاب کند.  بالعکس، اگر تابع هدف دوم در اولویت باشد، تصمیم‌گیرنده می‌تواند روش برنامه‌ریزی آرمانی را برای حل مسئله انتخاب کند.

شکل 11، زمان محاسبه روش  lexicographic weighted Tchebycheff و پنج روش MODM را نشان می‌دهد. که روش lexicographic weighted Tchebycheff  نسبت به روش MODM  زمان محاسبه‌ی کمتری نیاز دارد. سومین حل بهینه پارتو بدست آمده با استفاده از روش lexicographic weighted Tchebycheff ، بهترین حل از نظر محاسبه‌ی زمانی‌است.

  

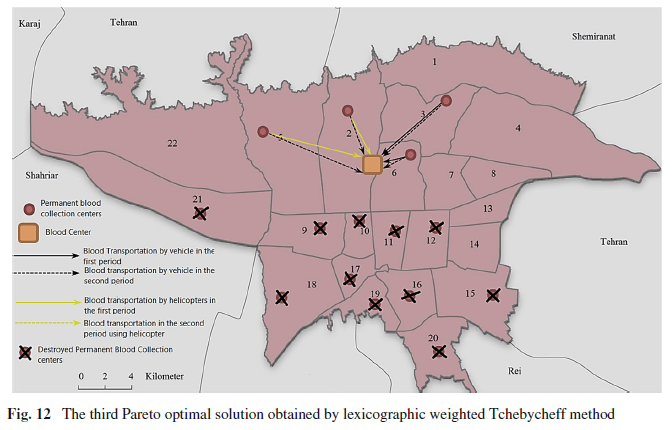
شکل 12 محل مراکز دائم جمع‌آوری خون و انتقال خون جمع آوری شده از مراکز جمع آوری را در دو دوره اول پس از زلزله 7.8 ریشتر نشان می‌دهد. علاوه بر این، مراکز جمع‌آوری دائم در مناطق 9 ، 10 ، 11 ، 12 ، 15 ، 16 ، 17 ، 18 ، 19 ، 20 ، 21 منطقه در اثر زلزله ویران می‌شوند. نتایج حاصل از اجرای مدل نشان می‌دهد که در دوره اول (24 ساعت اول)، به دلیل افزایش قابل توجه تقاضای خون در 24 ساعت اول، لازم است که خون سریعا جمع‌آوری شده و از مراکز جمع آوری به مرکز خون منتقل شود.  بنابراین، براساس نتایج، استفاده از وسایل حمل‌ونقل سریع مانند بالگردها در مراکز جمع آوری خون 2 و 5 ضروری است.

تجزیه و تحلیل حساسیت

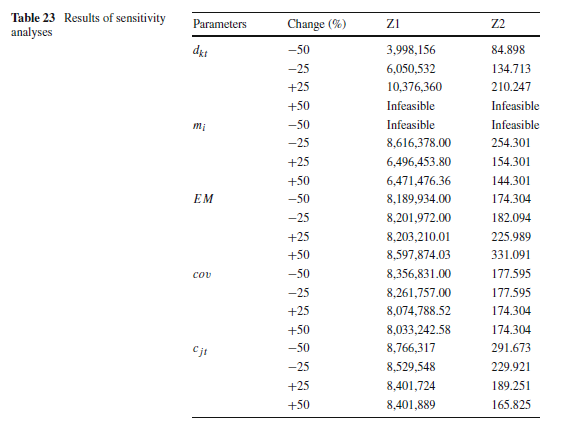
جدول 23، نتایج حاصل از تغییر پارامترها را نشان می‌دهد.

افزایش تقاضا باعث افزایش هر دو تابع هدف می‌شود و افزایش به میزان 50٪ + باعث غیرموجه شدن مسئله می‌شود. علاوه بر این، تغییر کوچکی در تقاضا منجر به ایجاد تغییر در هر دو مقدار تابع هدف می‌شود.

افزایش در mi باعث کاهش مقادیر توابع هدف می‌شود و کاهش 50 درصدی منجر به  غیرموجه شدن مسئله می‌شود.

افزایش EM  مقدار هر دو تابع هدف را افزایش می‌دهد. بدیهی است که زمین لرزه‌هایی با شدت بزرگتر، تلفات و تخریب بیشتری دارد. بنابراین، بیشتر مراکز جمع‌آوری دائم از بین می‌روند. این نتیجه منجر به افزایش قابل توجه در هزینه‌های زنجیره تأمین و زمان مورد نیاز برای انتقال خون جمع‌آوری شده به مراکز خون می‌شود.

افزایش cov هر دو مقدار توابع هدف را کاهش می‌دهد. این بدان معناست که بیشتر گروه‌های اهدا‌کننده تحت پوشش قرار می‌گیرند و نیازی به ایجاد مراکز جدید جمع‌آوری دائم برای جمع‌آوری خون از گروه‌های اهدا‌کننده نخواهد بود.

نتایج ، افزایش پارامترهای ظرفیت تسهیل دائم و شعاع پوشش، مقدار توابع هدف را به میزان قابل توجهی کاهش می‌دهد. بنابراین، تصمیم‌گیرنده می‌تواند کل هزینه‌های زنجیره تأمین و همچنین کل زمان حمل‌ونقل را کاهش دهد.

نتیجه‌گیری

در این مطالعه، یک مدل ریاضی چند هدفه برای طراحی شبکه زنجیره تامین خون در زلزله تهیه شده است. برای اولین بار در ادبیات حوزه، شعاع تخریب زلزله در مدل ریاضی در نظر گرفته شد تا هنگام وقوع زلزله شدید، یک زنجیره تأمین استوار طراحی شود. علاوه بر این، دو نوع وسیله انتقال خون برای انتقال خون جمع‌آوری شده از مراکز جمع آوری به مراکز خون تعیین شده است. همچنین سرعت، ظرفیت و تعداد وسایل نقلیه موجود در هر مکان متفاوت بوده است. طبیعتاً ، طراحی شبکه زنجیره تامین خون یک مسئله تصمیم‌گیری چند معیاره است، زیرا در تصمیم‌گیری در مورد محل‌ها و حمل‌ونقل بین آن‌ها ، اهداف متناقضی وجود دارد. مدل این تحقیق با هدف به حداقل رساندن زمان و هزینه کل در شبکه زنجیره تامین خون، ارائه شده‌است. حل‌های مختلف بهینه پارتو برای این مسئله بدست آمد، زیرا تصمیم‌گیرنده ممکن است بر اساس اهمیت هر تابع هدف، ترجیحات مختلفی داشته باشد.این مدل در شهر تهران، پایتخت ایران اجرا شد. در این مطالعه 22 ناحیه از شهر تهران مورد بررسی قرار گرفت که کاندیدای مراکز جمع‌آوری دائم و سیار می‌باشند. برای هر محل، وسایل حمل‌و‌نقل مختلف با ظرفیت و سرعت متفاوت برای انتقال خون از مراکز جمع آوری به مرکز خون در نظر گرفته شده بود. این مدل با استفاده از نرم افزار GAMS و با استفاده از روش‌های مختلف بهینه‌سازی چند هدفه حل شد و حل‌های مختلف بهینه Pareto بدست آمد. نتایج نشان داد که در دوره اول (24 ساعت) استفاده از وسایل حمل‌ونقل سریع مانند بالگردها به دلیل افزایش قابل توجه در پارامتر تقاضا ضروری است..  همچنین، نتایج نشان داد که سطح موجودی اولیه در مرکز خون برای تأمین تقاضا در 24 ساعت اول از اهمیت بسیاری برخوردار است. علاوه بر این ، مدل ریاضی مشخص کرد که برخی از مراکز جمع‌آوری خون در اثر زلزله نابود شده‌اند و به تصمیم‌گیرنده و خدمات بهداشتی و درمانی کمک می‌کند زنجیره تأمین خون استوارتری را طراحی کنند. نتایج نشان داد که با افزایش شعاع پوشش و ظرفیت مراکز جمع آوری خون، می توان کل زمان حمل‌و‌نقل و کل هزینه‌های زنجیره تأمین را به میزان قابل توجهی کاهش داد.