مدیریت زنجیره تامین خون: بهینه‌سازی استوار، ریسک اختلال و سازگاری گروه خونی (مطالعه موردی) _ مقاله ششم

چکیده

با توجه به شرایط نامشخص از جمله عدم‌قطعیت تقاضای خون و اختلال در تسهیلات، و همچنین به دلیل ماهیت نامشخص فرآورده‌های خونی مانند طول عمر فسادپذیری، گروه‌های خونی مجزا و سازگاری  ABO-Rh (D)و اولویت قوانین در بین این گروه‌ها،  این مقاله با هدف کمک به زنجیره های تامین خون تحت عدم‌قطعیت ارائه شده است. در این راستا ، این مقاله یک مدل برنامه‌ریزی تصادفی دو سطحی دو هدفه برای مدیریت زنجیره تأمین گلبول‌های قرمز ایجاد می‌کند. این مدل، تصمیمات مربوط به مکانیابی-تخصیص و مدیریت موجودی را بهینه تعیین می‌کند و هدف اول آن به حداقل رساندن هزینه کل زنجیره تأمین شامل هزینه‌های ثابت، هزینه‌های عملیاتی، هزینه‌های نگهداری موجودی، هزینه‌های ضایعات و هزینه‌های حمل‌ونقل و هدف دوم، به حداقل رساندن سطح تعویض برای ارائه خدمات انتقال خون ایمن‌تر است.  برای بررسی عدم‌قطعیت زنجیره تامین خون، یک روش بهینه سازی روباست برای مقابله با عدم‌قطعیت پارامترها ابداع شده است و از روش TH برای ساخت مدل دو هدف قابل استفاده است. سپس یک مطالعه موردی واقعی از شهر مشهد، در ایران، برای نشان دادن کاربرد مدل و همچنین رویکردهای حل آن، انجام شده و در نهایت ، نتایج محاسباتی ارائه و مورد بحث قرار گرفته است.

کلید واژه‌ها: زنجیره تامین خون، برنامه‌ریزی چند هدفه، بهینه‌سازی استوار، ریسک اختلال، گروه خونی سازگار

 

مقدمه

می‌توان گفت یک سیستم بهداشت و درمان کارآمد باید شامل یک برنامه مناسب برای مدیریت زنجیره تامین خون باشد. هدف نهایی زنجیره تامین خون، تأمین خون ایمن و کافی با توجه به پیچیدگی و هزینه‌های مرتبط با آن می‌باشد. اهداکنندگان داوطلب، منابع خون هستند و از آنجا که اهدای خون رایگان است، ممکن است تصور شود که هزینه تأمین خون حداقل است، در حالی که عوامل متعددی مانند پیشرفت‌های تکنولوژیکی، پیری جمعیت هزینه‌هایی را به صنعت مراقبت‌های بهداشتی تحمیل می‌کنند. فساد‌پذیری فرآورده‌های خون و تمایز در  طول ماندگاری آن‌ها، عدم‌قطعیت تامین و تقاضا خون باعث پیچیدگی زنجیره تامین می‌شود.

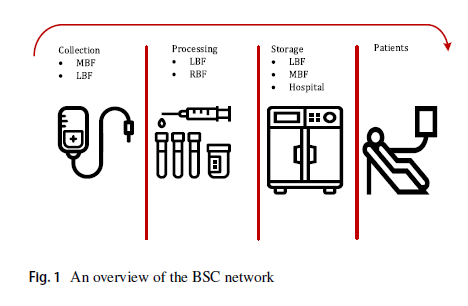
به طور کلی، زنجیره تامین خون (BSC) شامل جمع‌آوری، آزمایش و فرآوری، ذخیره‌سازی و همچنین توزیع خون در نقاط تقاضا  می‌باشد . در فرآیند جمع‌آوری، اهداکنندگان داوطلب برای اهدای خون به تسهیلات محلی خون (LBF) و تسهیلات سیار خون (MBF)  مراجعه می‌کنند (LBF تسهیلات جمع‌آوری ثابت هستند). با توجه به محدود بودن منابع خون، مسئله تخصیص این منبع بخش اساسی در برنامه‌ریزی BSC دارد.  در مرحله فرآوری، واحدهای اهدا شده از نظر عفونت‌ها و آلزژی‌ها تست می‌شوند. پس از کنارگذاشته شدن واحدهای عفونی، واحدهای ایمن به اجزای خون، از جمله گلبول‌های قرمز (RBCs) ، پلاسما و پلاکت‌ها تقسیم می‌شوند . فرآوری در LBF و تسهیلات خون منطقه‌ای (RBF)  انجام می‌شود. در مرحله بعد، هر یک از این محصولات فرآوری شده به بیمارستان منتقل می‌شوند. محصولات فرآوری در بیمارستان‌ها، LBF و RBF نگهداری می‌شوند. شکل 1 نمای کلی از شبکه مربوطه را نشان می‌دهد.

یکی از فرآورده‌های مهم خون RBC است که بخش عمده‌ی تزریق خون را تشکیل می‌دهد. علاوه بر این، RBC   تقریباً 50٪ از حجم خون بدن را تشکیل می‌دهد که به دلیل عدم وجود آنتی ژن‌ها به چهار گروه A، B، AB و O طبقه‌بندی می‌شوند. برخی از این گروه‌های خونی با یکدیگر سازگار هستند و می‌توانند جایگزین شوند. اگرچه جایگزینی منجر به جلوگیری از کمبود می‌شود ولی هدف این است که  هر بیمار تا حد امکان گروه خونی خود را استفاده کند.

تسهیلات زنجیره تأمین همواره در معرض اختلالات غیرعمدی یا حتی عمدی قرار دارد. هنگام  اختلال، هزینه‌های اضافی بر زنجیره تأمین تحمیل می‌شود و عواقب آن مانند کمبود موجودی کالا و تأخیر در سفارش، بر کل سیستم تأثیر منفی می‌گذارد.  این پژوهش با هدف پاسخ به سؤالات زیر انجام می‌شود:

1.      برای به حداقل رساندن واحدهای منسوخ و کمبود چه راهکارهایی باید اتخاذ شود؟

2.      محل MBF  کجاست و چگونه می‌توان آن‌ها را به مراکز خون اختصاص داد تا تقاضا را به بهترین وجه برآورده کند؟

3.      برای  مقابله ریسک‌ها و عدم‌قطعیت‌ها چه رویکردهایی اعمال می‌شود؟  چگونه می‌توان مدل ریاضی را برای کاهش این ریسک‌ها تدوین کرد؟

برای نزدیک‌تر شدن به واقعیت، اختلالات در اجزای شبکه، MBF و LBF در نظر گرفته شده‌است. این مقاله یک مدل دو مرحله‌ای استوار-تصادفی دو هدفه برای مدیریت زنجیره تامین خون یکپارچه ارائه شده است. مدل به طور همزمان دو هدف را دنبال می‌کند که هدف اول کل هزینه‌های زنجیره خون را به حداقل می‌رساند و هدف دوم تعداد واحدهای خون جایگزین را به حداقل می‌رساند.

خلاصه مرور ادبیات

ویژگی‌های مقاله:

·         ارائه یک مدل دو هدفه با توجه به ویژگی‌های مختلف از جمله ویژگی‌های فسادپذیری و گزینه‌های سازگاریABO-Rh

·         توجه به عدم‌قطعیت تقاضا و اختلال در تامین شبکه مربوطه.

·         پرداختن به سناریوهای تقاضا و اختلال با استفاده از یک روش بهینه‌سازی استوار.

·         بررسی مدل ارائه شده در یک مطالعه موردی واقعی در شهر مشهد در ایران.

بیان مسئله و فرمول ریاضی

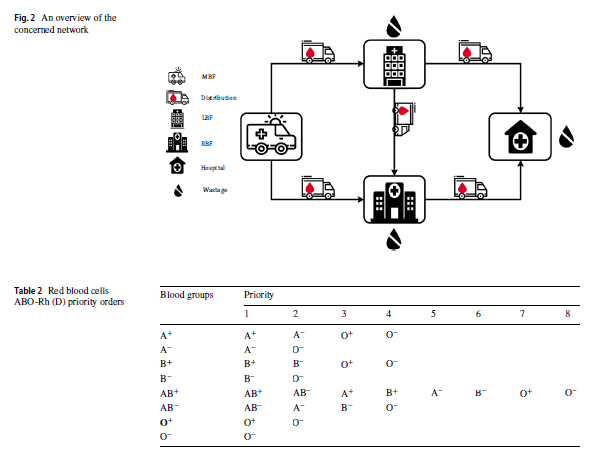
این مقاله به طراحی و برنامه‌ریزی شبکه زنجیره تأمین RBC که شامل تسهیلات سیار خون MBF، مراکز محلی خون LBF، تسهیلات منطقه‌ای خون RBF و بیمارستان‌ها به عنوان نقاط تقاضا می‌باشد. مراحل این شبکه جمع‌آوری خون، آزمایش و تولید، ذخیره و توزیع می‌باشد. در MBF، خون از اهداکنندگان گرفته‌می‌شود و سپس به LBF و RBF منتقل می‌شود. در LBF ، خون جمع آوری، فرآوری و ذخیره می‌شود. در صورت معاینه بیشتر‌، بخشی از خون جمع آوری شده در LBF به دلیل تجهیزات پیشرفته‌تر در RBF، به RBF منقل می‌شود. خون را می‌توان در RBF پردازش و ذخیره کرد. سرانجام، خون فرآوری شده براساس تقاضا به بیمارستان‌ها منتقل می‌شود. همچنین می‌توان خون را در بیمارستان‌ها ذخیره کرد تا بر اساس عمر باقی مانده آن‌ها مورد استفاده قرار گیرد. شکل 2 نمای کلی از شبکه مربوط را نشان می‌دهد. همانطور که در شکل 2 نشان داده شده است، در هر کدام از LBF ، RBF  و بیمارستان می‌تواند ضایعات داشته باشند. در این مقاله، تقاضا نامشخص است و میزان عرضه تحت سناریوهای اختلال، متغیر است. هشت گروه خون برای RBCs در نظر گرفته شده است، و مطابق جدول2،  سازگاری ABO-Rh (D) در تعیین خون تزریقی به بیماران گنجانیده شده است و  بهتر است برای هر نوع خون، همان گروه خونی استفاده شود تا از واکنش‌های ناسازگار جلوگیری شود. با توجه به این موضوع، یک جریمه به هر واحد جایگزین اختصاص داده می‌شود، اولویت جایگزینی گروه‌های خونی در جدول 2 نشان داده شده است. در این مقاله فرضیات زیر در نظر گرفته شده است

·         میزان تقاضای خون نامشخص است و ممکن است اختلال در مراکز جمع‌آوری خون به وجود آید.

·         تعداد محدودی از MBF در دسترس است.

·         در هر دوره کلیه تقاضاهای بیمارستان‌ها برآورده می‌شود.

·         ظرفیت تولید در LBF و RBF محدود است و ظرفیت ذخیره‌سازی در LBF ، RBF  و بیمارستان‌ها محدود است.

·         هزینه ضایعات یک واحد خون در LBF ، RBF  و بیمارستان‌ها در نظر گرفته می‌شود.

·         فسادپذیری RBCs و همچنین قانون اولویت سازگاری ABO-Rh (D)  در نظر گرفته شده است و سیاست FIFO در سیستم موجودی در نظر گرفته شده است تا واحدهای منسوخ شده را به حداقل برساند.

این مقاله با هدف تعیین تصمیمات زیر ارائه شده‌است:

·         تعداد و محل MBF و تخصیص خون جمع‌آوری شده در MBF به هر LBF یا RBF.

·         مقدار خون فرآوری شده در LBF و RBF ، مقدار خون منتقل شده از LBF و RBF به بیمارستان‌ها و مقدار خون هدایت شده از LBF به RBF.

·         سطح موجودی خون و تعداد واحدهای منسوخ شده در LBF ، RBF  و بیمارستان‌ها.

·         تعداد و نوع واحدهای خونی جایگزین.

 

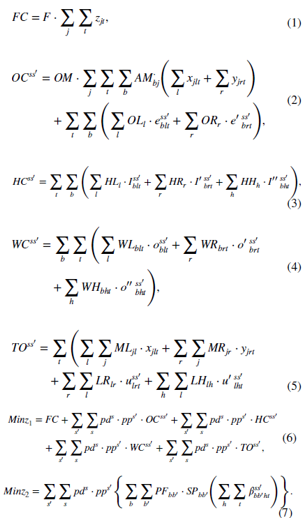
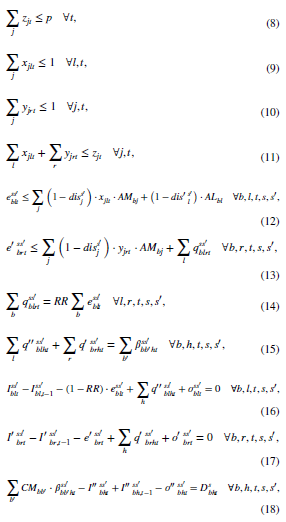
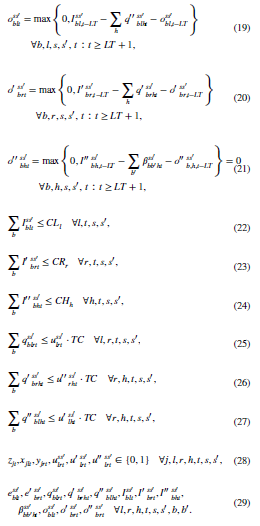
اولین تابع هدف:

معادله  (1) ، هزینه‌های ثابت حرکت MBF بین مناطق کاندید

معادله  (2)، هزینه‌های عملیاتی  در MBF ، LBF  و RBF

معادله  (3)،  هزینه نگهداری LBF ، RBF  و بیمارستان‌ها

معادله  (4)، هزینه‌های ضایعات در LBF ، RBF  و بیمارستان‌ها

معادله  (5)،  حمل‌ونقل از MBF به LBF و RBF ، از LBF به RBF و از LBF و RBF به بیمارستان انجام می‌شود.

معادله  (6)، کل هزینه‌های فوق در شبکه مورد بررسی به حداقل می‌رسند.

معادله  (7)، تابع هدف دوم، تعداد واحدهای جایگزین RBCs را به حداقل‌می‌رساند این هدف با تعیین جریمه برای هر جایگزین و در نظر گرفتن قوانین اولویتی ABO-Rh (D) حاصل می‌شود.

محدودیت (8) نشان می‌دهد که تعداد MBF موجود محدود هستند.

محدودیت (9) و (10) اختصاص هر MBF به نباید بیش از یک LBF یا RBF در هر دوره را تضمین می‌کند.

محدودیت (11) بیان می‌کند که هر MBF را می‌توان به LBF یا RBF اختصاص داد.

محدودیت (12) و (13) تعداد واحدهای خونی فرآوری شده در MBF و LBF را به تعداد واحدهای خون دسترس تحت هر سناریو محدود می‌کند.

محدودیت (14) نشان می‌دهد که یک میزان ثابت از خدمات انتقال LBF باید به LBF  تغییر مسیر دهند.

محدودیت (15) دلالت بر این دارد که مقدار کافی خون برای تأمین تمام تقاضاها بدون مواجهه با کمبود، جمع‌آوری می‌شود.

محدودیت‌های (16) -(18) معادلات تعادل موجودی خون در LBF ، RBF و بیمارستان‌ها در هر دوره و تحت هر سناریو است.

محدودیت‌های (19) -(21) تضمین می‌کنند که سیاست FIFO با توجه به ماندگاری آن‌ها، در مدیریت موجودی اعمال می‌شود.

محدودیت‌های (22) - (24) ظرفیت موجودی هر LBF ، RBF  و بیمارستان را در هر دوره و تحت هر سناریو نشان می‌دهد. محدودیت‌های (25) - (27) ظرفیت حمل‌ونقل را تضمین می‌کنند.

محدودیت‌های (28) و (29) دلالت بر دامنه متغیرهای تصمیم‌گیری دارند.

روش حل

مدل ارائه شده یک مدل برنامه‌ریزی تصادفی دو سطحی است. ماهیت تصادفی مدل که ناشی از عدم‌قطعیت تقاضا و اختلال است، حل مدل را پیچیده‌تر می‌کند. یک رویکرد دو فازی برای بررسی  BSC ارائه شده است:

در فاز 1، یک مدل بهینه‌سازی استوار برای مقابله با عد‌قطعیت پارامترهای ارائه شده است.

در فاز 2 ، یک رویکرد برنامه‌ریزی چندهدفه فازی تعاملی، به نام TH ، برای تبدیل مدل پیشنهادی به یک مدل تک هدفه استفاده می‌شود.

فاز 1: بهینه‌سازی استوار

استحکام زنجیره تامین خون در اثر ریسک‌های ناشی از عدم‌قطعیت در پارامترهایی مانند تقاضا و اختلالات، تهدید می‌شود. اختلالات موجود در مراکز جمع‌آوری خون بر میزان خونرسانی تأثیر می‌گذارد و باعث تاخیر در سفارش می‌شود. این ناسازگاری ممکن است به کمبود منجر شود که میزان مرگ و میر را افزایش می‌دهد. در چنین شرایط نامشخصی، استفاده از یک روش مناسب برای به دست آوردن مقدار بهینه توابع هدف بسیار مهم است. در این راستا، برای غلبه بر این اشکال، در مدل پیشنهادی از بهینه‌سازی استوار استفاده شده است. برای مقابله با عدم قطعیت، چندین رویکرد استوار پیشنهاد شده است. مدل استوار به شرح زیر است:

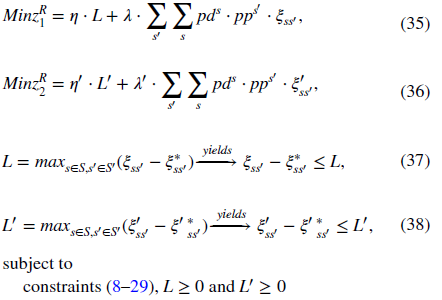
فاز 2: رویکرد حل فازی تعاملی

در مرحله اول یک مدل برنامه‌ریزی خطی عدد صحیح مختلط دو هدفه تصادفی ارائه شده است. در مرحله دوم، یک بهینه‌سازی استوار برای مدل اعمال می‌شود و اکنون، یک رویکرد کارآمد برای مقابله با مدل برنامه‌ریزی دو هدفه ارائه شده است. به همین دلیل، یک رویکرد برنامه‌ریزی فازی تعاملی چند هدفه به دلیل توانایی آن‌ در ارائه درجه رضایتمندی برای هر تابع هدف مورد استفاده قرار می‌گیرد. این روش که توسط ترابی و حسینی  با نام TH معرفی شده است، جواب‌های غیرغالب را ارائه می‌دهد. که بطور خلاصه مدل تک هدف زیر را ارائه می‌دهد:

 

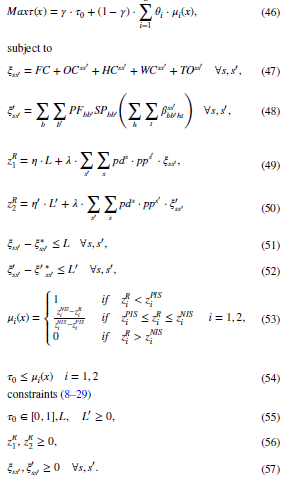
مطالعه موردی

در این مقاله از یک مطالعه موردی در شهر مشهد واقع در شمال شرقی ایران استفاده شده است. مشهد دومین شهر پرجمعیت ایران و دومین شهر بزرگ از لحاظ مساحت است. براساس سوابق سرشماری در سال 2016 ، مشهد دارای 3001184 نفر جمعیت است که به دلیل مهاجرت و بازدید میلیون‌ها زائر در حال افزایش است. در این راستا ، مدیریت و برنامه‌ریزی زنجیره تامین تأثیر خون در مشهد، به عنوان یک شهر پرجمعیت و بزرگ، از اهمیت بالایی برخوردار است.

محیط نامشخص در BSC نتایج متفاوتی ایجاد می‌کند که می‌تواند منجر به کمبود و ضایعات خون شود. درنظر گرفتن سناریوها در BSC به داشتن آینده‌ای بهتر و برنامه‌ریزی بهتر در صورت بروز هر سناریو کمک می‌کند. در BSC پیشنهادی، سه سناریو تقاضا بر اساس تقاضای هفتگی در بیمارستان‌ها با سطح پایین، متوسط ​​و بالا در نظر گرفته شده است.  علاوه بر این، سه سناریو اختلال براساس داده‌های تاریخی و نظر متخصصان ارائه شده است. بنابراین، 9 سناریو وجود دارد که منجر به کاهش ضایعات و کمبود در BSC می‌شود.

نتایج محاسباتی

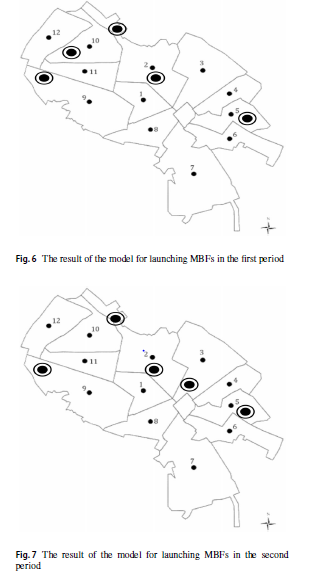
در این بخش، مدل با استفاده از داده های واقعی شهر مشهد حل می شود که مکان های پیشنهادی برای استقرارMBF  در شکل‌های 6 و 7 برای دوره اول و دوم به تصویر کشیده شده است.

طبق شکل 6 ، در دوره اول، 5 تا MBF برای جمع‌آوری خون در مناطق 2 ، 5 ، 9 و 10 مستقر شده‌اند و همانطور که نشان دادیم، 2 تا MBF بر اساس نتایج مدل در منطقه 2 مستقر می‌شوند.

در دوره دوم،  5 تا MBF برای جمع‌آوری خون استفاده می‌شود که 4 مورد از آن‌ها در همان محل دوره اول باقی می‌مانند و یکی از آن‌ها از منطقه 10 به منطقه 3 منتقل می‌شود.

 

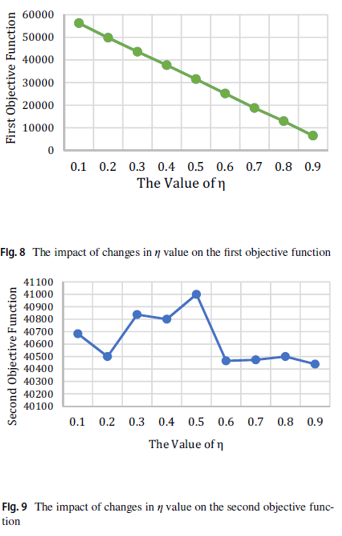
شکل 8 نشان می‌دهد که با افزایش مقدار η ،  با عث کاهش مداوم در مقدار تابع هدف اول می‌شود. این امر به دلیل افزایش η باعث می شود.

شکل 9،  نشان می‌دهد که مقدار تابع هدف دوم مستقیماً با مقدار η همراه نیست و در مقدار تابع هدف دوم ایجاد نوسان می‌کند.

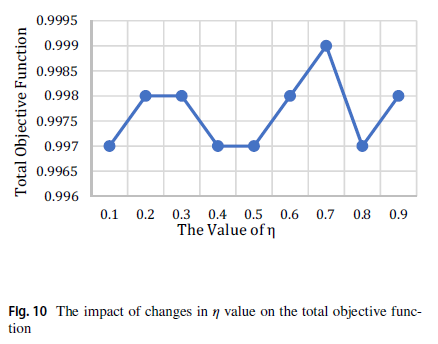
شکل 10 تأثیر را بر η تابع هدف کل توصیف می‌کند.

همانطور که در این شکل نشان داده شده است، بهترین مقدار برای تابع هدف کل زمانی حاصل می شود که مقدار η برابر 0.7  باشد.

همانطور که در شکل 8 و 9 نشان داده شده است،  مقدار تغییرات η ، مقدار توابع هدف اول و دوم را بطور جداگانه تغییر می‌دهد و این تغییرات منجر به نوسان در مقدار تابع هدف کل می‌شود و هدف این است که برای بدست آوردن نتایج بهینه، بهترین مقدار پارامتر η  انتخاب شود. 

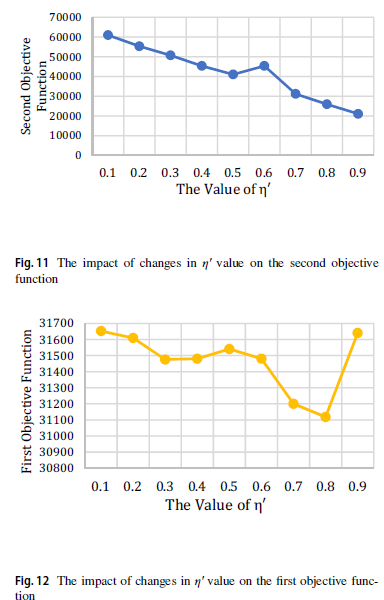
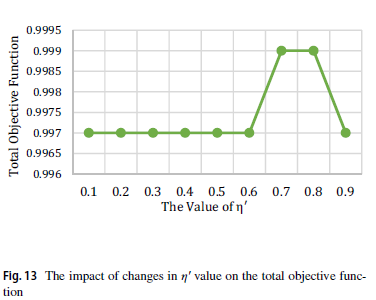
شکل 11 ، 12 و 13 نشان‌دهنده تأثیر مقادیر مختلف ́η بر تابع هدف دوم ، تابع هدف اول و تابع هدف کل است. همانطور که مشاهده می‌شود، مقدار تابع هدف دوم با افزایش مقدار ́η کاهش می‌یابد و مقدار تابع هدف اول را بطور غیرخطی تغییر می‌دهد و همچنین، بهترین نتایج برای تابع هدف کل در ́η برابر 0.7 و 0.8  بدست می‌آید.

 

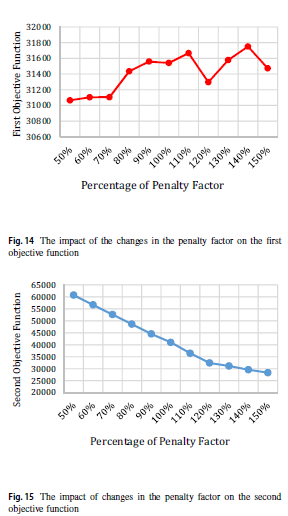
در این بخش، تأثیر عامل جریمه بر مقدار توابع هدف بررسی شده است. در این مقاله ، برای هر واحد خون جایگزین ، یک عامل جریمه در نظر گرفته شده است. هدف از در نظر گرفتن جریمه استفاده کمتر از واحدهای جایگزین  است که منجر به تأمین خون ایمن‌تر برای بیماران می‌شود زیرا جایگزینی ممکن است منجر به عواقبی مانند عفونت‌ها و آلرژی‌ها شود.

 همانطور که در شکل 15 نشان داده شده است، با افزایش مقدار جریمه، تعداد واحدهای جایگزین کاهش یافته و بر این اساس، مقدار تابع هدف دوم کاهش می‌یابد. در این دستورالعمل، افزایش ضریب جریمه منجر به استفاده از همان گروه خون بیماران برای تزریق و تا حد امکان از جایگزینی خون اجتناب می‌شود.

تأثیر ضریب افزایش جریمه در اولین تابع هدف در شکل 14 نشان داده شده است. نرخ افزایشی جریمه منجر به استفاده کمتر از واحد جایگزین می‌شود. به این ترتیب، شبکه باید خون بیشتری برای تأمین همان گروه‌های خون، برای بیماران فراهم کند که منجر به افزایش هزینه‌ها می‌شود.

نتیجه‌گیری

در این مقاله یک الگوی برنامه‌ریزی تصادفی دوسطحی دو هدفه برای مدیریت و برنامه‌ریزی یک زنجیره تأمین یکپارچه RBC با گردآوری سهم‌های زیر ارائه شده است.  مدل ارائه شده دارای دو سطحی است که در سطح اول، تصمیمات تاکتیکی مانند مکان و تعداد MBF مشخص می‌شود و مرحله دوم شامل تصمیمات مربوط به موجودی و تولید است. برای نزدیک‌تر شدن به واقعیت، این اختلال در مرکز جمع‌آوری خون در نظر گرفته شده است که بر میزان خون رسانی تأثیر می‌گذارد. با استفاده از بهینه‌سازی چند هدفه، تصمیم‌گیرند‌ه می‌تواند معیارهای مختلفی در تصمیم‌گیری خود داشته باشند که در این مدل، دو هدف در نظر گرفته می‌شود.

تابع هدف اول کل هزینه زنجیره تأمین و تابع هدف دوم تعداد واحدهای جایگزینی را حداقل می‌رساند. برای حل مدل دوهدفه از روش TH  استفاده شده است. در این روش درجه مطلوبیت برای هر تابع هدف تعیین می‌شود برای مقابله با عدم قطعیت، از یک رویکرد بهینه‌سازی استوار مبتنی بر سناریو استفاده شده است که در آن دو سناریو تحت عنوان سناریوی تقاضا و سناریوی اختلال در نظر گرفته می‌شوند. سناریوهای تقاضای خون و اختلال،  ظرفیت تسهیلات جمع‌آوری خون را تحت تأثیر قرار می‌دهند و در نتیجه بر میزان تأمین خون تأثیر می‌گذارند. در آخر، اعتبار مدل با استفاده از مطالعه موردی در ایران مورد بررسی قرار گرفت.