طراحی و بهینه‌سازی شبکه زنجیره تأمین پایدار برای بانک پلاکت خون تحت عدم‌قطعیت (مقاله هفتم)

چکیده

در این مقاله یک شبکه مدل بهینه‌سازی احتمالی برای زنجیره تامین خون پایدار چند دور‌ه‌ای و چند هدفه با داده‌های غیرقطعی در هنگام بروز بحران ارائه شده است. اجزای زنجیره تامین در این تحقیق گروه‌های اهداکننده، مراکز جمع‌آوری خون، مراکز توزیع و بیمارستان‌ها هستند. اهداف شبکه، به حداقل رساندن هزینه کل و اثرات زیست محیطی و به حداکثر رساندن تأثیرات اجتماعی می‌باشد. سپس از روش اپسیلون محدودیت برای تبدیل مدل ریاضی چند هدفه به مدل تک هدف استفاده می‌شود. برای حل مسائل در اندازه‌های بزرگ، یک الگوریتم فرابتکاری، یعنی الگوریتم تبرید شبیه‌سازی شده SA برای حل مدل ارائه شده است. برخی از نمونه‌های عددی حل و ارزیابی شده و عملکرد الگوریتم SA با الگوریتم جستجوی هارمونیHS مقایسه می‌شود. سرانجام، نتایج به دست آمده مورد بحث قرار می‌گیرد و نتیجه‌گیری ارائه می‌شود.

کلید واژه‌ها: مدیریت زنجیره تامین، بانک پلاکت خون، پایداری، برنامه‌ریزی احتمالی، عدم‌قطعیت

 

مقدمه

طراحی شبکه زنجیره تأمین یا SCND تأثیر برجسته‌ای بر عملکرد زنجیره تأمین دارد. این شبکه، تعداد و محل تسهیلات، ظرفیت‌های آن‌ها و همچنین تخصیص جریان اطلاعات و مواد را تحت تأثیر قرار می دهد. SCND یک مسئله مهم در تصمیمات تاکتیکی و عملیاتی در مدیریت زنجیره تأمین است . نگرانی های فزاینده برای پاسخگویی به الزامات زیست محیطی ، اجتماعی و قانونی ، شرکت ها را وادار می کند تا تأثیرات طراحی زنجیره تأمین پایدار SSC را بر محیط زیست و جامعه در نظر بگیرند . یک مفهوم مهم در مورد پایداری، مسئولیت اجتماعی شرکت‌ها (CSR)  است. خون انسان یک منبع حیاتی و نادر است. این ماده از بدن انسان تامین می‌شود و در حال حاضر، هیچ محصول جایگزین خون وجود ندارد.

در بین فرآورده‌های مختلف خون، پلاکت ها از قابلیت فسادپذیری بالایی برخوردار هستند، زیرا فقط پنج روز قبل از فاسدشدن می‌توان آن‌ها را نجات داد. به همین دلیل پلاکت‌ها منابع با ارزشی هستند. آن‌ها فقط در موارد خاص مورد نیاز هستند، اما در شرایط بحران به واحدهای متعددی از آن‌ها احتیاج داریم؛ در نتیجه، تقاضا پلاکت‌ها بسیار متغیر است.

توجه به عدم‌قطعیت در طراحی و بهینه‌سازی زنجیره‌های تأمین ضروری است. در یک زنجیره تأمین، بحران، یکی از منابع عدم قطعیت است و هنگامی اتفاق می‌افتد که فعالیت یک یا چند عضو زنجیره قطع شود و منجر به ایجاد اختلالات عمده در جریان عادی سرویس‌دهی شود.

نوآوری‌های مقاله:

         ·            تهیه یک الگوی جامع طراحی زنجیره تامین پلاکت خون (شامل موجودی، مکانیابی، تخصیص، مسیریابی) با ادغام پایداری در فرآیند تصمیم‌گیری.

         ·            از روش افرزیس برای تهیه پلاکت‌های خون به عنوان روشی کارآمد استفاده می‎شود.

         ·            به دلیل عدم‌قطعیت ذاتی داده‌های ورودی، از تکنیک جدید برنامه‎‌ریزی احتمالی پیشنهاد شده برای مدیریت عدم‌قطعیت مدل، با توجه به نگرش‌های مختلف تصمیم‌گیرندگان استفاده شده است.

         ·            ما در مدل دو نوع از بیماران را در نظر می‌گیریم.  بیماران نوع 1 کسانی هستند که به خون جوان احتیاج دارند (پلاکت‌هایی با سن کمتر از 3 روز).  بیماران نوع 2 کسانی هستند که از هر نوع خون استفاده می‌کنند.

         ·            یکی از مزیت‌های مهم مدل ما ، بررسی یک موضوع عملی در این زمینه است. هنگامی که خون قدیمی (پلاکت‌های دارای بیش از 4 روز) برای نوع 2 وجود نداشته باشد ، می‌توان با در نظر گرفتن هزینه جریمه از خون جوان استفاده کرد، و هنگامی که خون جوان برای نوع 1 وجود نداشته باشد ، می توان  از خون قدیمی استفاده کرد که ممکن است عوارض جانبی داشته باشد که منجر به ناسازگاری شود. بنابراین جریمه در نظر گرفته شده است.

تعریف مسئله و مدل ریاضی

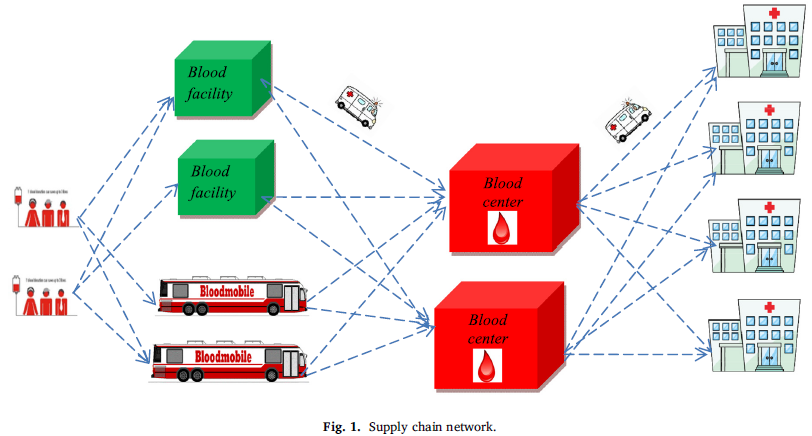
شبکه زنجیره تامین خون و جریان در میان اجزای شبکه در شکل 1 نشان داده شده است. بخش اول مربوط به فعالیت‌های اهدای خون است. واحدهای خون از گروه‌های مختلف اهداکننده، از طریق تسهیل خون ثابت یا سیار جمع‌آوری می‌شوند.

تسهیلات خون ثابت و مراکز خون از بین مکان‌های بالقوه موجود انتخاب می‌شوند. پس از ثبت نام، کلیه اهداکنندگان به مراکز خون مراجعه می‌کنند از طریق یک روند غربالگری معاینه می‌شوند تا از انتقال بیماری‌های ناشی از تزریق خون جلوگیری کنند.

علاوه بر این، قبل از انتقال خون، آزمایش سازگاری برای جلوگیری از پیامدهای ناسازگاری انجام می‌شود. هر وسیله نقلیه از مرکز خون شروع می‌کند و مسیر مشخصی را برای ارائه خدمات به بیمارستان‌های معین می‌پیماید و به همان مرکز خون برمی‌گردد. پلاکت‌های خون توسط  آفرزیس به دست می‌آیند. آفرزیس پلاکت یک روش پیشرفته برای جمع‌آوری و تهیه پلاکت‌های خون و اجزای آن‌ها است. سپس باقیمانده اجزای خون به بدن انسان بازگردانده می‌شود.

              

فرضیات مدل

         ·            طول عمر پلاکت ها شامل پنج روز (دو روز برای روند آزمایش) است.

         ·            بین درخواست سفارش بیمارستان و تحویل واحهای خون زمانی وجود ندارد.

         ·            وسایل نقلیه مختلف با ظرفیت‎های مختلف وجود دارد.

         ·            در هر دوره با یک وسیله نقلیه حداکثر یک بار بیمارستان یا مرکز خون قابل بازدید است.

         ·            حداکثر یک وسیله نقلیه به هر مسیر اختصاص داده می‌شود.

         ·            طول هر دوره یک روز است.

         ·            تسهیلات خون، مراکز خون و بیمارستان‌ها ظرفیت‌های محدودی دارند.

         ·            هر سفر باید در همان مرکز خون مستقر شروع و پایان یابد.

         ·            سنین واحدهای پلاکت خون شناخته شده است.  پلاکت هایی با سن کمتر از 3 روز جوان محسوب می‌شوند.

         ·            دو نوع عدم‌قطعیت از جمله عدم‌قطعیت ذاتی و عدم قطعیت ناشی از بحران (به عنوان مثال ، زلزله ، سیل و آتش سوزی) وجود دارد.

         ·            مکان بیمارستان‌ها و گروه‌های اهدا‌کننده ثابت است.

         ·            کمبود مجاز است، و هزینه کمبود به عنوان هزینه تقاضا برطرف نشده تعریف می‌شود.

هدف مدل ما تعیین و مشخص نمودن تسهیلات خون و  مراکز خون، اندازه هر محموله و کارآمدترین مسیرهای وسیله نقلیه برای به دست آوردن حداقل هزینه کل، با توجه به اثرات زیست محیطی و اجتماعی شبکه (یعنی تسهیلات خون، مراکز توزیع خون و بیمارستان‌ها) است. ما یک مدل SCND  عدد صحیح مختلط چند هدفه پیشنهاد می‌کنیم که در آن مکان‌ها، سطح موجودی و بهترین مسیرها را با توجه به اهداف تعیین می‌کنیم.

 

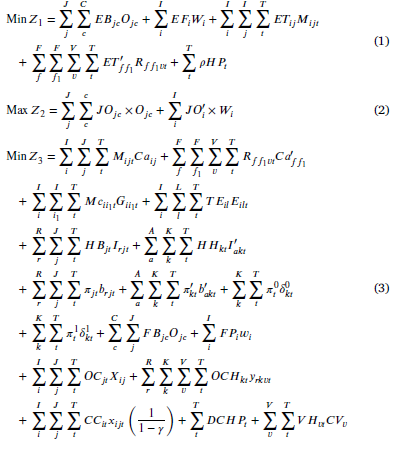
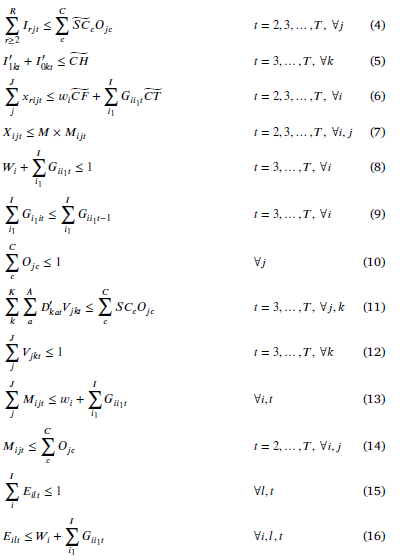
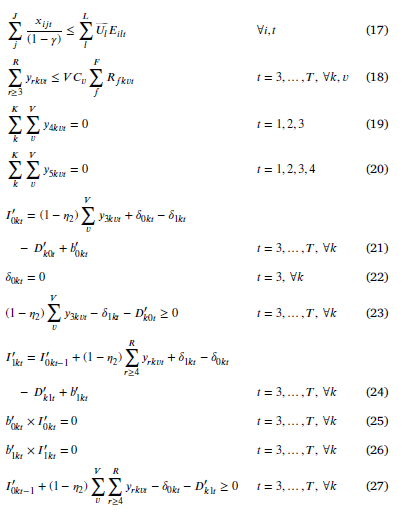
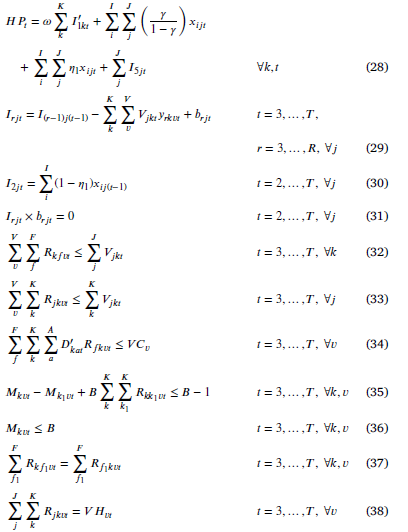
تابع هدف (1) کل اثرات زیست محیطی را به حداقل می‌رساند. عبارات اول و دوم تأثیرات زیست محیطی ناشی از ایجاد مراکز خونی و تسهیلات دائم خون در هر مکان بالقوه را نشان می‌دهد. عبارات سوم و چهارم تأثیرات زیست محیطی در حمل‌ونقل واحدهای جمع‌آوری شده از تسهیلات خون به مراکز خون و از مراکز خون به بیمارستان‌ها را نشان می‌دهد. آخرین عبارت هزینه جریمه ناشی از دفع ضایعات خون است.

تابع هدف (2)، تأثیرات کل اجتماعی را به حداکثر می‌رساند. عبارات اول و دوم مربوط به مشاغل ثابت (سمت‌هایی مانند مدیران مستقل از ظرفیت تسهیلات خون) و مشاغل متغیر است.مشاغل متغیر آن دسته از مشاغلی هستند که کاملاً به ظرفیت تسهیلات متکی هستند. به عنوان مثال، یک مرکز خونی با اندازه بیشتر به کارگران یا کارمندان بیشتری نسبت به تسهیلات کوچکتر نیاز دارد.

تابع هدف (3)، کل هزینه‌های متغیر و ثابت موجود در شبکه را به حداقل می‌رساند. عبارت اول تا چهارم هزینه حمل‌ونقل، عبارات پنجم و ششم هزینه‌های نگهداری خون را در بانک‌های خون، عبارات هفتم و هشتم هزینه کمبود خون، عبارات نهم و دهم هزینه‌های ناسازگاری و عدم‌تطابق، عبارات یازدهم و دوازدهم برای هزینه‌های ثابت تأسیس مراکز خون و تسهیلات خون، عبارات سیزدهم و چهاردهم هزینه‌های عملیاتی یا تولید خون و سه عبارت آخر به ترتیب هزینه‌های دفع ضایعات خون و هزینه‌های تنظیم وسیله نقلیه نشان می‌دهد.

محدودیت‌های (4) و (5) تصریح می‌کند که سطح موجودی یک مرکز خون یا بیمارستان باید متناسب با ظرفیت‌شان باشد.

محدودیت (6) میزان ارسال خون از تسهیل خون به مراکز خونی را محدود می‌کند.

محدودیت (7) ایجاب می‌کند که اگر تسهیل خون به هیچ مرکز خون اختصاص نیابد، هیچ خونی از این تسهیل خون به مرکز خون ارسال نمی‌شود.

محدودیت (8) باعث می‌شود که حداکثر یک تسهیل خون در هر محل مستقر شود.

محدودیت (9) تحمیل می‌کند که تسهیلات کوتاه مدت خون فقط در صورتی که یک تسهیل آنجا مستقر شده باشد می‌توانند از یک محل حرکت کنند.

محدودیت (10) تضمین می‌کند که در هر مکان j ، فقط یک مرکز خون با یک اندازه می‌تواند ایجاد شود.

محدودیت (11) تضمین می‌کند که تقاضای هر بیمارستان باید از ظرفیت مرکز خون تخصیص داده شده، کمتر مساوی باشد.

محدودیت (12) تصریح می‌کند که نمی توان هر بیمارستان را به بیش از یک مرکز خون اختصاص داد.

نابرابری (13) تضمین می کند که اگر یک تسهیل خون در محل i مستقر شود، هر مرکز خون به یک تسهیل خون تخصیص داده می‌شود.

محدودیت (14) ایجاب می‌کند که در صورت بسته شدن مرکز خون، هیچ تسهیل خون به آن اختصاص نیابد.

محدودیت (15) تضمین می‌کند که هر گروه اهداکننده به حداکثر یک تسهیل خون اختصاص می‌یابد.

محدودیت (16) موجب می‌شود که اهداکنندگان خون به تسهیلات خون مستقر اختصاص یابد.

محدودیت (17) حداکثر خون هر تسهیل خون  باید از حداکثر میزان خونرسانی از گروه اهداکننده تخصیص داده شده، کمتر مساوی باشد.

محدودیت (18) نشان می‌دهد که خون تحویل داده شده به هر بیمارستان بستگی به نوع وسیله نقلیه تخصیص یافته برای تور مربوطه دارد.

محدودیت‌های (19) و (20) زمان آماده‌سازی خون برای تحویل به هر بیمارستان را در نظر می‌گیرند.

محدودیت (21) تعادل موجودی خون جوان هر بیمارستان را نشان می‌دهد.

محدودیت (22) نشان می‌دهد که هیچ خون قدیمی برای ناسازگاری خون وجود ندارد.

محدودیت (23) نشان می‌دهد که مصرف خون جوان توسط بیماران نوع 2 منجر به کمبود خون جوان نمی‌شود.

محدودیت (24) تعادل موجودی خون قدیمی را در هر بیمارستان نشان می‌دهد.

محدودیت‌های (25) و (26) نشان می‌دهد که حداکثر یک متغیر می تواند مثبت باشد.

محدودیت (27) نشان می دهد که مصرف خون قدیمی توسط بیماران نوع 1 منجر به کمبود خون قدیمی نمی‌شود

محدودیت (28) کل خون غیرقابل استفاده یا خون از دست رفته در کل زنجیره تأمین محاسبه می‌کند.

محدودیت‌های (29) و (30) مربوط به میزان موجودی خون پایان دوره در مراکز خون هستند.

محدودیت (31) تضمین می‌کند که حداکثر یک متغیر می‌تواند مثبت باشد.

محدودیت‌های (32) و (33) تضمین می‌کند که هر بیمارستان و مرکز خون حداکثر یک بار قابل بازدید هستند.

محدودیت (34) مستلزم رعایت ظرفیت هر وسیله نقلیه است.

محدودیت (35)  برای از بین بردن زیر تور است و تضمین می‌کند که در هر دوره هر مشتری یک بار بازدید می‌شود و هیچ برگشتی نیز ندارد.

محدودیت (36) حداکثر مقدار متغیر کمکی مربوطه را نشان می‌دهد.

محدودیت (37) در هر دوره زمانی،جریان هر بیمارستان تحمیل می‌کندکه وسیله نقلیه به مرکز توزیع خود بازگردد.

محدودیت (38) نشان می‌دهد که هر وسیله نقلیه، حداکثر، یک مرکز خون را ترک می‌کند.

محدودیت (39) تحمیل می‌کند که مرکز خون j به بیمارستان k خدمات می‌دهد، اگر وسیله نقلیه v از j  به k رفنه‌باشد،

محدودیت (40) اطمینان حاصل می‌کند که هیچ ارتباطی بین مراکز خونی وجود ندارد و همچنین هیچ ارتباطی بین هر مرکز خون یا بیمارستان به خودی خود وجود ندارد.

محدودیت (41) تا (43) دامنه متغیرهای تصمیم‌گیری را تعریف می‌کند.

خطی سازی

نوع 1 ، ضرب متغیرهای عدد صحیح و باینری

محدودیت (29) ضرب متغیرهای عدد صحیح و باینری را نشان می‌دهد.  برای برای خطی‌سازی، آن را با محدودیت‌های (44)-(47) جایگزین می‌کنیم.

       

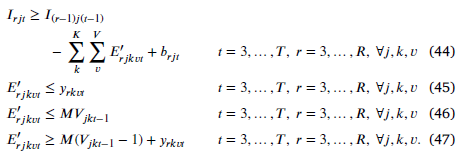
نوع 2 ، ضرب دو متغیر عدد صحیح

محدودیت‌های (31)، (25) و (26) را به محدودیت‌های زیر تبدیل می‌کنیم.

 

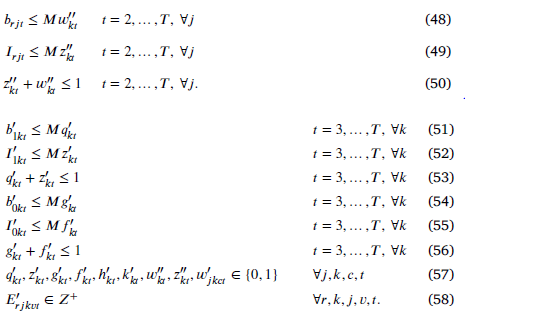
روش حل

از رویکرد برنامه‌ریزی احتمالی فازی برای عدم‌قطعیت پارامترها استفاده شده است.

و از روش اپسیلون محدودیت برای تیدیل کردن مدل چند هدفه به تک هدفه استفاده شده است. در این تکنیک، با در نظر گرفتن سایر توابع هدف به عنوان محدودیت‌های جدید، تابع اصلی بهینه شده است.

به دلیل پیچیدگی مدل ریاضی پیشنهادی، ما یک الگوریتم فراابتکاری، به نام الگوریتم تبرید شبیه‌سازی شده، برای حل مدل تک هدفه اعمال می‌کنیم. بنابراین، مسئله می‌تواند در یک زمان معقول، به ویژه برای نمونه‌هایی در اندازه بزرگ حل شود. بدون الگوریتم فراابتکاری، دستیابی به یک حل موجه در یک زمان قابل قبول غیرممکن است.

اعتبار‌سنجی

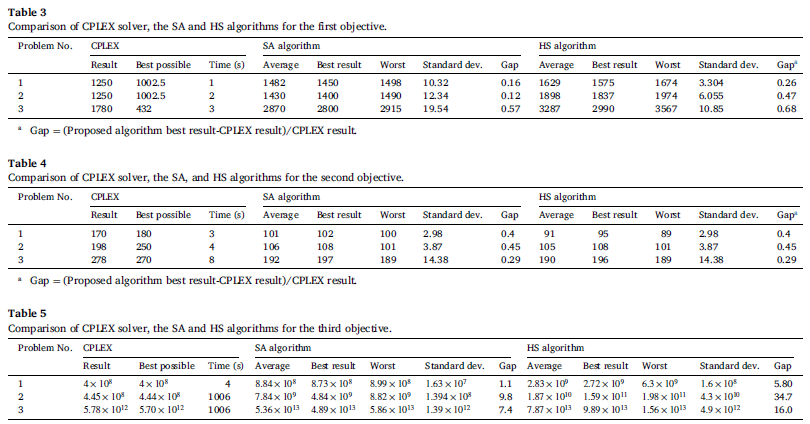
ما کارایی الگوریتم SA توسعه یافته را با نتایج CPLEX برای اعتبار سنجی مقایسه می‌کنیم. علاوه بر این، الگوریتم جستجوی هارمونی HS برای اعتبار سنجی الگوریتم از SA  استفاده شده است.

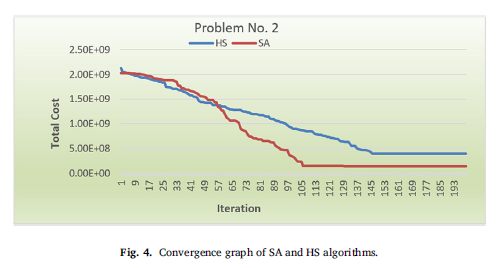
در اکثر موارد در جداول 3 تا 5، الگوریتم SA حل‌های نزدیک به جواب‌های CPLEX را تولید می‌کند.الگوریتم SA به طور واضح از  الگوریتم HS در مسائل تست بهتر است. معیار دیگر برای نشان دادن قدرت یک الگوریتم شاغل ، قدرت همگرا آن برای دستیابی به یک راه حل بهینه تقریباً نزدیک است که در شکل 4 مشاهده می شود، الگوریتم SA با سرعت بیشتری به حل بهتر همگرا می‌شود.

                                                                           

نتیجه گیری

طراحی شبکه زنجیره تامین خون نقش برجسته‌ای در مکانیابی و تخصیص تسهیلات خون دارد. به دلیل ماهیت فرآورده‌های خون، فسادپذیری مسئله مهمی در این زمینه است. در این مطالعه، ما یک فرمول برنامه‌ریزی خطی عدد صحیح مختلط برای طراحی و بهینه‌سازی SCND مربوط به فرآورده‌های خون با سه تابع هدف ارائه داده‌ایم. با توجه به وجود برخی پارامترهای ورودی غیردقیق شبکه زنجیره تأمین، ما یک مدل تحت عدم‌قطعیت تهیه کرده‌ایم. در این راستا از یک روش برنامه‌ریزی احتمالی فازی استفاده شده است. علاوه بر این، یک الگوریتم تبرید شبیه‌سازی شده و الگوریتم جستجوی هارمونی توسعه داده شده است. با استفاده از داده های تصادفی تولید شده، حل‌های به دست آمده توسط CPLEX و دو الگوریتم پیشنهادی مقایسه شده‌اند.