طراحی شبکه زنجیره تامین خون با توجه به سازگاری گروه خونی تحت عدم قطعیت (مقاله ششم)

چکیده:

در این مقاله به طراحی شبکه زنجیره تامین خون (SC) با توجه به سازگاری گروه خونی پرداخته شده است. برای این منظور، یک مدل برنامه ریزی ریاضی دو هدفی تهیه شده است که هزینه کل و همچنین حداکثر تقاضای برآورده نشده را به حداقل می رساند. با توجه به ماهیت  غیر قطعی برخی پارامترهای ورودی، دو مدل برنامه ریزی غیر قطعی مبتنی بر اندازه گیری اعتبار ارائه شده است. سپس داده های یک مطالعه موردی واقعی برای نشان دادن کاربرد و عملکرد مدل های پیشنهادی و همچنین اعتبارسنجی رویکرد برنامه ریزی استوار پیشنهادی مورد استفاده قرار می گیرد. نتایج به دست آمده نشان از برتری مدلهای توسعه یافته و صرفه جویی قابل توجهی در هزینه نسبت به شبکه SC خون موجود دارد.

کلید واژه ها: طراحی شبکه زنجیره تامین خون، طراحی زنجیره تامین، روش های فازی، برنامه ریزی مختلط خطی عدد صحیح

مقدمه:
مدیریت خون یک مسئله نگرانی خاص برای نسل بشر است. بر خلاف سایر منابع قابل تعویض، نیاز به اهدای خون و محصولات مشتق از آن همیشه وجود داشته است.  متداول ترین اجزای حاصل از خون کامل (WB) عبارتند از: پلاسما (PLS)، گلبول قرمز خون (RBC) و پلاکت (PLT)  که  PLT ذخیره شده می تواند تا پنج روز مورد استفاده قرار گیرد در حالی که زمان ماندگاری برای PLS تا یک سال اعلام شده است. زمان ماندگاری مجاز برای RBC تا 42 روز اعلام شده است، در حالی که مطالعات قبلی نشان می دهد در صورت ذخیره RBC طولانی تر از 14 روز، خطر مرگ در حین جراحی قلب به میزان قابل توجهی افزایش خواهد یافت. بطور کلی شبکه زنجیره تامین خون از مراکز اصلی امکانات موقتی / سیار و مراکز آزمایشگاهی تشکیل شده است. مراکز اصلی وظیفه جمع آوری خون با ظرفیت بسیار بالای ذخیره سازی و فناوری را بر عهده دارند. ایجاد این امکانات معمولاً نیاز به سرمایه گذاری شدید دارد. در صورت انتقال خون باید خون با همان گروه مشابه به بیمار تزریق شود. در مواقع اضطراری یا هنگامی که گروه خونی درخواستی در دسترس نباشد، می توان از یک گروه خونی سازگار استفاده کرد. برای محصولات مشتق شده، سازگاری گروه خونی هرکدام یکسان نیست.

با توجه به ماهیت پویا و غیر قطعی SC خون، برخی از پارامترهای ورودی از قبیل میزان عرضه، تقاضا و زمان سفر با عدم قطعیت مواجه می شوند و در نتیجه، تصمیمات طراحی شبکه ممکن است تحت تأثیر قرار گیرد. بنابراین، مسئله با پارامترهای ورودی غیر قطعی و ریسک های مرتبط با آن باید با دقت مورد توجه قرار گیرد. هدف از این مقاله معرفی یک الگوی برنامه ریزی مختلط عدد صحیح دو هدف برای مسئله تخصیص مکان چند دوره در یک سیستم SC خون با توجه به به حداقل رساندن کل هزینه ها و همچنین حداکثر تقاضای برآورده نشده می باشد.

سهم اصلی این مقاله، که آن را  متمایز می کند، به شرح زیر است:

·       طراحی یک شبکه خون چند دوره ای جدید SC که نوسانات عرضه و تقاضا را تنظیم می کند.

·       پیشنهاد دو رویکرد برنامه ریزی استوار برای مقابله با عدم قطعیت معرفتی در مسئله مورد نظر

·       با توجه به قابلیت آسیب پذیری اجزای مشتق شده و همچنین سازگاری گروه های خونی که کاربرد عملی مدل پیشنهادی را به میزان قابل توجهی تقویت می کند.

·       استفاده از مدل پیشنهادی در یک مطالعه موردی واقعی برای نشان دادن کاربرد روشهای پیشنهادی

تعریف و فرمول مسئله

اهدای خون معمولاً از طریق امکانات دائمی یا موقت انجام می شود. مراکز دائمی در مقایسه با امکانات موقتی، نقش کلیدی در کل شبکه SC بازی می کنند. در نتیجه، مراکز اصلی مجهز به سطح و ظرفیت بالاتری از فناوری برای کاهش بیماری های عفونی و انتقال خون و همچنین کاهش خطرات تحمیل شده برای اهدا کنندگان هستند.

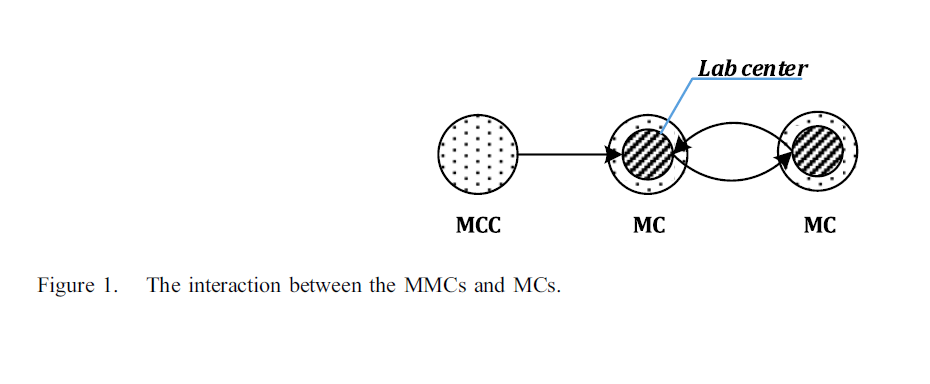
قابل ذکر است که ایجاد یک مرکز دائمی بسیار پرهزینه تر از یک مرکز موقت است. بنابراین، استفاده از امکانات موقت برای تأمین خواسته های پراکنده در بسیاری از موارد واقعی قابل توجیه است. کلیه بسته های خون دریافت شده برای استخراج  اجزای مورد نیاز، به مراکز آزمایشگاهی که در داخل مراکز دائمی قرار دارند ارسال می شود. بنابراین شبکه مربوطه یک شبکه تک محصوله قبل از مناطق آزمایشگاهی است و پس از آن به SC چند محصول تبدیل می شود. لازم به ذکر است که فقط تعدادی از مراکز اصلی شامل آزمایشگاه هایی هستند که MCC نامیده می شوند. سرانجام، تمام مؤلفه های مشتق شده به مناطق تقاضا ارسال می شوند. تعامل بین MCC ها و مراکز آزمایشگاه با امکان انتقال بین آزمایشگاه ها در شکل زیر نشان داده شده است. همانطور که قبلاً گفته شد، محصولات حاصل از بسته های خونی قابل تجزیه هستند. بنابراین، تنظیم این موضوع در شبکه مربوطه جنبه دیگری دارد که باید در فرموله کردن مسئله مورد توجه قرار گیرد.

 مدل برنامه ریزی ریاضی

با استفاده از چارچوب مدل سازی ارائه شده در این بخش، یک مدل برنامه ریزی ریاضی  برای طراحی شبکه خون SC پیشنهاد شده است. فرضیات و ساده سازی های در نظر گرفته شده در مدل ارائه شده به شرح زیر است:

·       محل مناطق گیرنده ثابت و شناخته شده است، در حالی که فقط مکان های کاندیدای مراکز موقت و دائمی از پیش تعیین شده اند.

·       سازگاری گروه خونی  هر محصول مورد توجه قرار می گیرد.

·       محصول واحد قبل از جداسازی از طریق شبکه ارسال می شود و پس از آن چندین محصول در SC منتقل می شود.

·       ماهیت پویا منابع و مطالبات باید تصمیمات برنامه ریزی را در چند دوره در نظر بگیرد.

·       زمان ماندگاری خون فقط در مسیرهای حمل و نقل در نظر گرفته می شود.

·       با توجه به درجه بالای عدم قطعیت معرفتی پارامترهای ورودی، عدم دقت پارامترها از طریق توزیع امکان در نظر گرفته می شود.

مدل قطعی پیشنهادی

تابع هدف (1): هزینه کل شامل هزینه های تأسیس مراکز دائمی و آزمایشگاهی و مکان یابی و هزینه های حرکت مراکز موقت در هر دوره و همچنین هزینه های جریان مواد را به حداقل می رساند.

تابع هدف دوم (2): درصدد کم کردن حداکثر تقاضای برآورده نشده محصولات مختلف در بین مناطق تقاضا در طول افق برنامه ریزی برای ایجاد تعادل مناسب و عادلانه بین مناطق تقاضا.

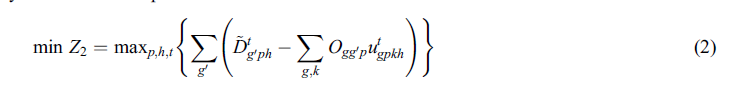
محدودیت های (3) تا (5): به حرکت تسهیلات موقت در هر دوره اشاره دارد. محدودیت (3) تضمین می کند که حداکثر یک مرکز موقت می تواند به هر مکان منتخب  j2 در هر دوره منتقل شود، در حالی که حرکت هر تسهیلات موقت به حداکثر یک مکان منتخب توسط مجموعه محدودیت 4 تضمین می شود. مجموعه محدودیت های (5) به امکان سنجی حرکت متوالی از محل کاندید  j1 تا j2 می پردازد. به عبارت دقیق تر، اگر این مرکز در دوره قبلی (آن جا جابجا شود) یک مکان موقت فقط می تواند به مکان بالقوه دیگری منتقل شود .(j1 → j2)

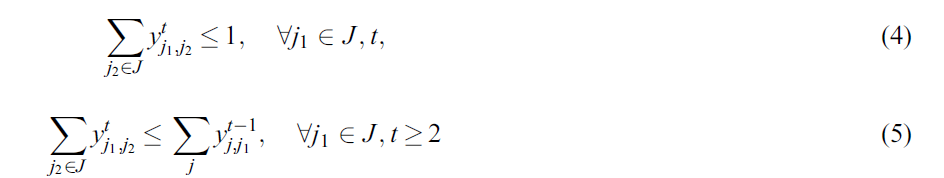
مجموعه محدودیت (6): نشان می دهد که در صورت اهدای خون، یک اهدا کننده فقط می تواند در یک زمان به یک مرکز موقت یا یک مرکز دائمی خون اهدا کند.

محدودیت های محدوده (7) تا (9): به ترتیب محدودیت های پوشش دهنده بین اهدا کنندگان و تسهیلات موقتی، اهدا کنندگان و مراکز دائمی و مراکز موقت و دائمی است. به عبارت دیگر، یک اهدا کننده فقط می تواند در یک مرکز موقت ( با توجه به محدودیت (7)) در صورتی که وی تحت شعاع پوشش تأسیسات قرار داشته باشد  )به عنوان مثال  (Rij ≤ r covered. همین مورد در مورد مجموعه های محدودیت (8) و (9) نیز صدق می کند.

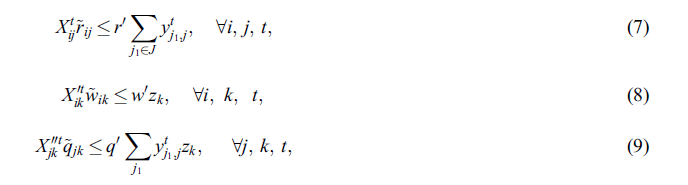
مجموعه های محدودیت (10) تا (12): تضمین می کنند که انتساب بین هر جفت گره فقط در صورت وجود جریان بین این گره ها امکان پذیر است. اختصاص اهداکنندگان به تسهیلات موقت، اهداکنندگان به مراکز دائمی و تسهیلات موقت به مراکز دائمی به ترتیب محدودیت های (10) ، (11) و (12) ارائه می شود.

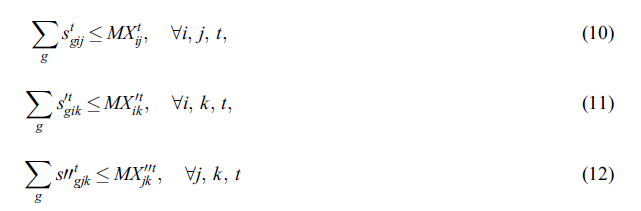
مجموعه های محدوده (13) تا (15): به ترتیب از محدودیت ظرفیت در مراکز دائمی، حجم خون در دسترس اهدا کنندگان و امکانات موقتی اطمینان حاصل می کنند.

مجموعه های محدودیت (16) و (17): به ترتیب تعادل جریان را در مراکز موقت و دائمی تضمین می کنند. به عبارت دیگر، معادله (16) تضمین می کند که در پایان هر دوره، کلیه خون اهدا شده در مراکز موقت به مراکز دائمی منتقل می شود. مجموعه محدودیت ها (17) اطمینان می دهد که تمام بسته های خون دریافت شده برای انتقال به مراکز آزمایشگاه فرستاده می شوند.

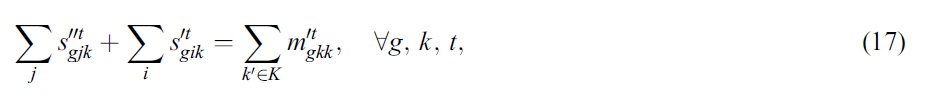مجموعه محدودیت (18) حداکثر حجم جریان حمل شده در هر دوره را محدود می کند، که برابر با کسری احتمالی از کل ورودی ها به مرکز آزمایشگاه است که در همان دوره با جریانهای خروجی خارج می شوند. از طرف دیگر، نشان می دهد این جریان تنها هنگامی امکان پذیر است که مرکز آزمایشگاه مربوطه باز باشد

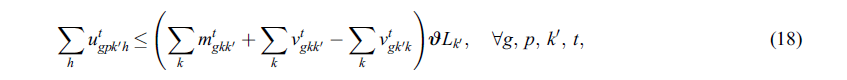
مجموعه محدودیت (19): محدودیت زمانی است که اطمینان حاصل می کند محصولات مشتق شده در کمتر از زمان فساد مربوطه به مناطق تقاضا منتقل می شوند.

 مجموعه محدودیت (20):  در صورت باز بودن مرکز آزمایشگاه مرتبط، ایجاد مرکز دائمی را تضمین می کند

مجموعه محدودیت (21): تضمین می کند که مقدار کل محصولات مشتق شده با گروه های خونی سازگار که باید جایگزین شوند از کل کالاهای منتقل شده به مناطق تقاضای تجاوز نمی کند.

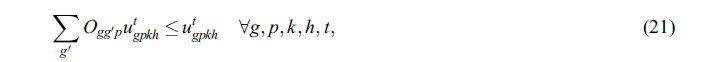
   محدودیتهای (22) و (23): محدودیتهای باینری، عدد صحیح و غیر منفی بودن را بر روی متغیرهای تصمیم گیری اعمال می کنند.

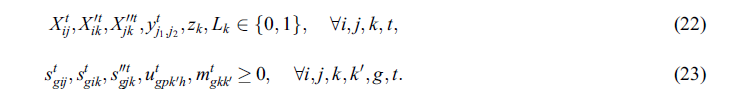
در محدودیت 24 و 25:  که y^`  تعداد کل امکانات خون موقت است. این مجموعه محدودیت ها تضمین می کند که تعداد کل تسهیلات موقتی در طول دوره های زمانی ثابت و برابر با تعداد بهینه تسهیلات محاسبه شده توسط مدل است.

 

برای تبدیل معادله (19): به شکل استاندارد ، Y_gpkh یک متغیر دودویی است. اگر u   نامنفی باشد یک در غیر این صورت 0 است. سپس می تواند به شرح زیر بازنویسی شود:

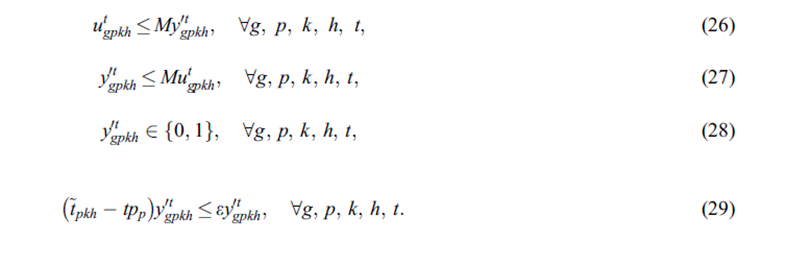
 خطی سازی

تابع هدف دوم و مجموعه های محدودیت (9) و (18) غیر خطی هستند. برای فرار از پیچیدگی چنین مدل غیرخطی، مدل به یک مدل خطی به شرح زیر تبدیل می شود:

خطی سازی تابع هدف

با توجه به ساختار حداقل حداکثر تابع هدف دوم، یک متغیر k مثبت برای تسهیل خطی سازی عملکرد هدف مورد نظر تعریف شده است. بر این اساس، این مدل را می توان به شرح زیر بازنویسی کرد:

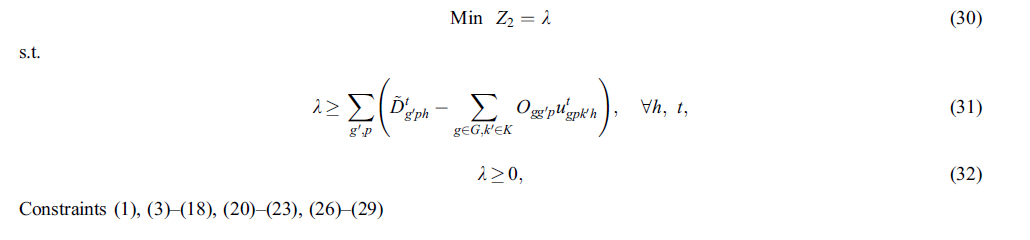
برای خطی سازی مجموعه محدودیت ها (9)، محصول متغیرهای باینری y وz   با یک متغیر جدید باینری تعریف شده. سپس، تبدیل محدودیت مربوطه به یک نسخه خطی از طریق محدودیت های زیر قابل دستیابی است.

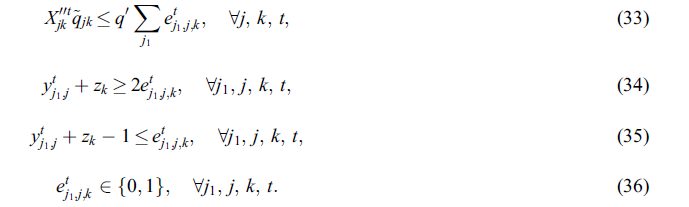
علاوه بر این، خطی سازی محدودیت (18) با مجموعه محدودیت های زیر می تواند به سادگی انجام شود.

روش حل:

همانطور که قبلاً ذکر شد، برخی از پارامترهای ورودی در مدل ارائه شده با عدم قطعیت معرفتی مواجه می شوند. ادبیات مرتبط نشان می دهد که رویکرد برنامه ریزی احتمالی بیشتر برای مقابله با پارامترهای ورودی مبهم استفاده می شود، در حالی که برنامه ریزی انعطاف پذیر برای مقابله با ارزش هدف انعطاف پذیر اهداف و محدودیت ها اعمال می شود. در میان روش های برنامه ریزی توسعه یافته امکان پذیر، برنامه نویسی محدودیت فازی یکی از ابزارهایی است که به طور گسترده مورد استفاده قرار می گیرد زیرا قادر است سطح اطمینان از محدودیت های شانس را بر اساس مفاهیم ریاضی فازی استوار کنترل کند، ضمن پشتیبانی از انواع مختلف اعداد فازی. با این حال، این رویکرد در عین حال از ضعف های زیادی مانند عدم کنترل انحراف تابع هدف از تابع برنامه ریزی شده آن و شیوه ذهنی این رویکرد در تعیین سطح اطمینان از محدودیت های شانس رنج می برد که نمی تواند ارزش مطلوب سطح اطمینان را تضمین کند. برای غلبه بر نواقص فوق الذکر در روشهای برنامه ریزی سنتی احتمالی، در این بخش یک مدل برنامه ریزی پایدار ترکیبی جدید مبتنی برای سنجش اعتبار پیشنهاد می کنیم.

 مدل برنامه ریزی محدودیت شانس فازی مبتنی بر اعتبار

اندازه گیری Cr یک اندازه گیری خود دوگانه است، یعنی هنگامی که اندازه گیری Cr مقادیر 0 یا 1 را بدست آورد، رویداد فازی مربوطه مطمئناً اتفاق می افتد یا شکست می یابد. برای راحت تر کار کردن، فرم فشره شده مدل پیشنهادی را به شرح زیر در نظر بگیرید:

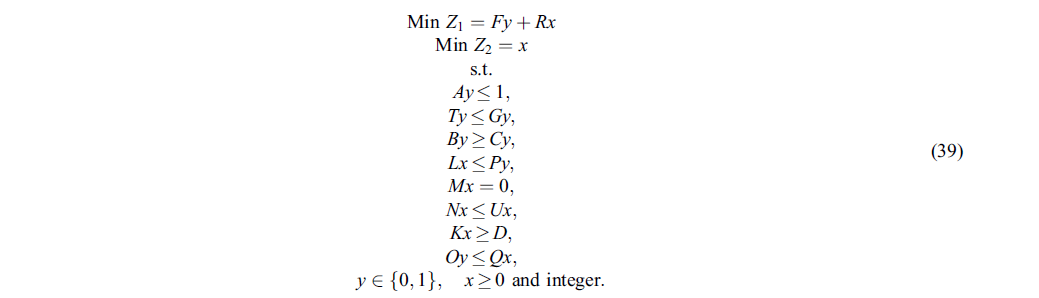
جایی که بردارهایF ، R و D به ترتیب با هزینه ثابت، هزینه متغیر و تقاضا مطابقت دارند. علاوه بر این، ماتریس هایA ، T، G ، B ، C ، L ، P ، M ، N ، U ، K ، O و Q ماتریس های ضرایب هستند و بردارهای y و x به ترتیب متغیرهای باینری و عدد صحیح را نشان می دهند. حال فرض کنید بردارهایF ،R و D و ماتریس ضرایب T که نشان دهنده زمان سفر بین گره ها است پارامترهای غیر قطعی در شکل فشرده شده مدل پیشنهادی هستند. علاوه بر این ، فرض کنید که پارامترها دارای عدم قطعیت دارای توزیع امکان ذوزنقه ای هستند که توسط چهار نقطه نشان داده شده است.

با توجه به Zhu and Zhang (2009)، برای قطعی سازی فرمول 40  به صورت زیر عمل میکنیم:

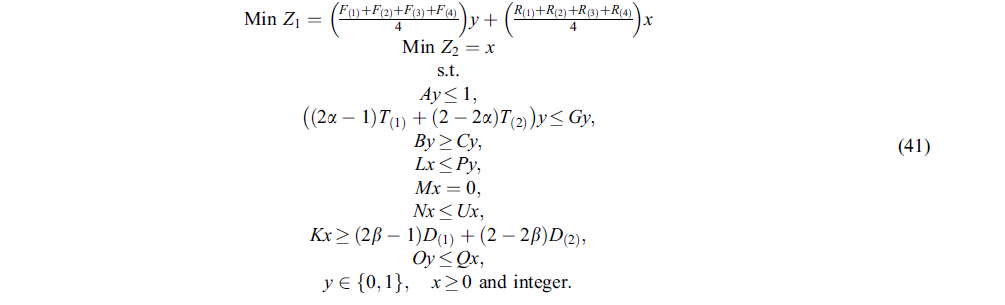
در مدل های برنامه ریزی محدودیت برای شانس، حداقل میزان اطمینان از محدودیت های شانس به دلیل ترجیحات DM باید تعیین شود. بنابراین، مدل نمی تواند بهینه بودن سطح اطمینان را تضمین کند. علاوه بر این، معمولاً DM مقدار سطوح اطمینان را در یک روش تعاملی و خطای تعاملی تعیین می کند که منجر به فرایند زمانبری می شود. از آنجا که مدل (40) نسبت به انحراف تابع هدف از مقدار مورد انتظار خود حساس نیست، ممکن است در موارد واقعی  خطرات بالایی و هزینه های اضافی به DM تحمیل شود. برای مقابله با چنین ناکارآمدی ها، استفاده از رویکرد برنامه ریزی استوار کاملاً قابل توجیه خواهد بود.

مدل برنامه ریزی استوار مبتنی بر اعتبار

اگر یک مسئله بهینه سازی  برای همه مقادیر ممکن پارامترهای ناصحیح (یعنی استواری شدنی) امکان پذیر باشد و مقدار تابع هدف مربوطه نزدیک به مقدار مطلوب باشد یا حداقل انحراف (نامطلوب) از مقدار بهینه برای (تقریبا) تمام مقادیر ممکن پارامترهای ورودی غیر قطعی (یعنی استواری بهینگی) داشته باشد یک مسئله استوار  محسوب میشود. در برنامه ریزی کلاسیک استوار احتمالی، اندازه گیری Nec  برای مقابله با محدودیت های غیر قطعی استفاده می شود. با توجه به مزایای اندازه گیری Cr  در مقایسه با سایر اقدامات فازی( به عنوان مثال اقدامات Nec و Pos )،  یک مدل برنامه ریزی جدید احتمالی را بر اساس اندازه گیری Cr به شرح زیر ارائه می دهیم:

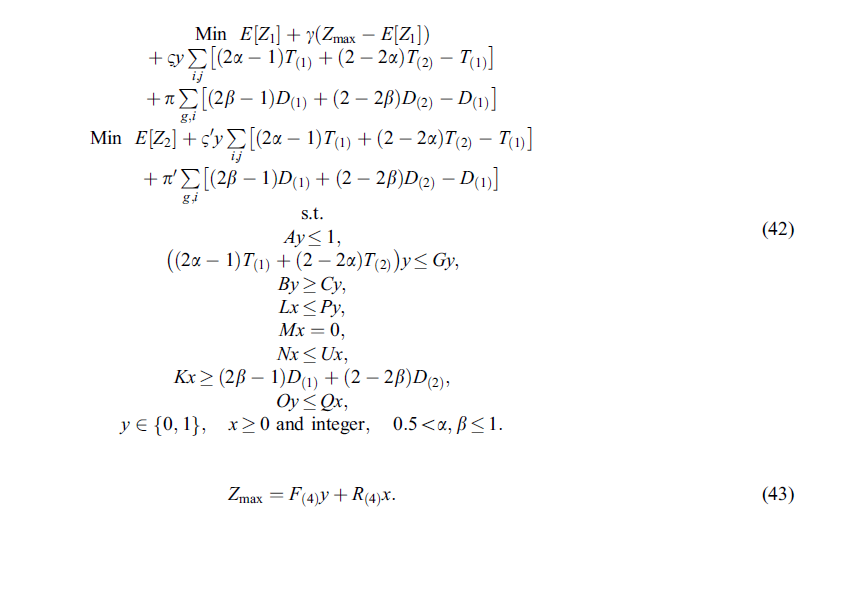
قسمت اول هر دو تابع هدف سعی در به حداقل رساندن مقدار میانگین توابع هدف اصلی مربوطه دارد. قسمت دوم در تابع هدف اول تفاوت بین حداکثر مقدار ممکن و میانگین ارزش تابع هدف اصلی دارد. این قسمت انحراف در تابع هدف را از میانگین تابع هدف برنامه ریزی شده کنترل می کند. به عبارت دیگر، این قسمت، استواری بهینگی را کنترل می کند. همانطور که مشاهده می شود، نسخه خطی تابع هدف دوم هیچ پارامتر فازی ندارد. بنابراین، نیازی برای کنترل استواری بهینگی نیست. دو قسمت آخر در هر دو تابع، قابلیت شدنی بودن دو محدودیت احتمال را تنظیم می کند. این موارد اختلاف بین بدترین مقدار پارامترهای غیر قطعی و مقدار انتخاب شده توسط مدل برای استفاده در محدودیت های شانس را به حداقل می رساند.

کمبود یا هزینه ظرفیت استفاده نشده، نمونه ای از پارامترهای مجازات است که به عنوان پارامترهای رایج در ادبیات شناخته می شوند. با توجه به مدل PCCP ، در اینجا سطح اطمینان از محدودیت های شانس، متغیرها هستند و مقادیر آنها در مدل بهینه  میشود.

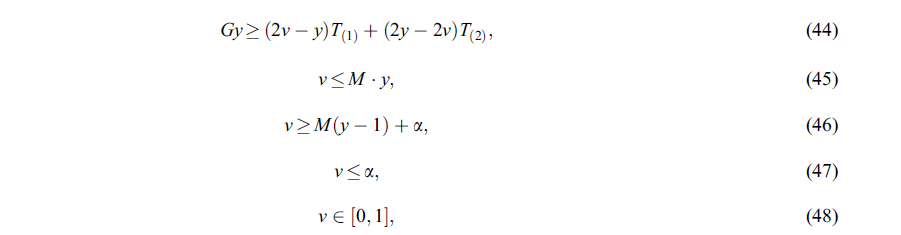
پس تابع هدف به صورت زیر بازنویسی میشود:

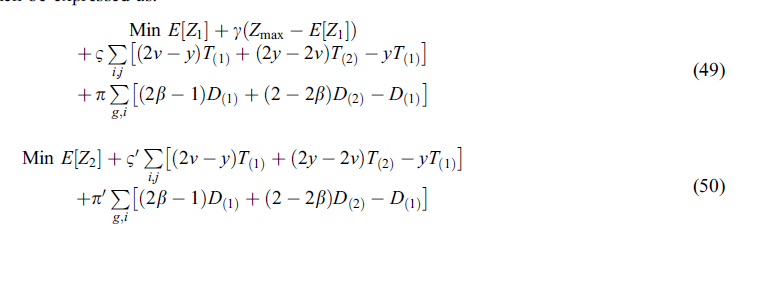
مدل برنامه ریزی استوار مبتنی بر اعتبار اصلاح شده

در فرمول مدل برنامه ریزی استوارمبتنی بر اعتبار (CRRP)، احتمال نقض تقریباً نادیده گرفته می شود و نقض محدودیت با روشی بسیار محافظه کار محاسبه می شود. برای جلوگیری از بروز چنین مشکلی و ایجاد یک رویکردی که  کمتر محافظه کار باشد؛ یک نسخه اصلاح شده از مدل CCRP یعنی MCRPP پیشنهاد شده است که اجز تابع هدف دوم، به شرح زیر تدوین شده است.

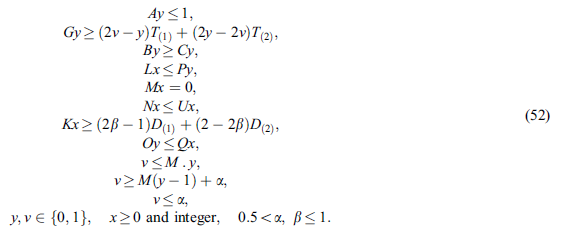
پس با توجه به رویکرد  TH مدل چند هدفه را به تک هدفه قطعی تبدیل میکنند.

نتیجه گیری:

با توجه به اینکه خون  یک محصول مهم در زندگی انسان میباشد؛ در این مقاله یک مدل MILP دو هدف برای طراحی شبکه آزمایش خون با توجه به سازگاری ABO برای اولین بار ارائه شده است. به منظور به حداکثر رساندن بهره وری سیستم و همچنین جنبه های اجتماعی، تابع هدف در نظر گرفته شده سعی در به حداقل رساندن هزینه کل و همچنین حداکثر تقاضای برآورده نشده در بین مناطق تقاضا دارند. با توجه به ماهیت دارای عدم قطعیت برخی پارامترهای مهم ورودی، دو رویکرد احتمالی مبتنی بر اعتبار توسعه یافته و مطلوبیت راه حل های آنها از طریق یک مطالعه موردی واقعی در ایران ارزیابی شده است. نتایج عددی بدست آمده برتری مدل های پیشنهادی برنامه ریزی استوار پیشنهادی را نشان می دهد زیرا صرفه جویی قابل توجهی در هزینه با مدل CRPP در مقایسه با شبکه SC خون موجود در مورد مورد نظر حاصل می شود. به طور دقیق تر، برای مقادیر که جریمه کمتری دارند؛ MCRPP عملکرد بهتری نسبت به سایر مدلهای مورد مطالعه نشان می دهد، در حالی که وقتی مقادیر جریمه بالاتر باشد، CRPP از سایر موارد بهتر است.