جمع آوری خون به روش آفرزیس یا خون کامل؟ رویکرد بهینه سازی تصادفی چند هدفه ( مقاله دهم)

چکیده

در زنجیره تامین خون چندین تکنولوژی برای جمع آوری و پردازش خون در دسترس است. این تکنولوژی ها از نظر هزینه و کارایی متفاوت هستند؛ به عنوان مثال، جمع آوری به روش افرزیس به تجهیزات بسیار گران قیمت نیاز دارد، اما بازده فرآورده های خونی به طور قابل توجهی بیشتر از جمع آوری به روش خون کامل است. از مشکلات استراتژیک زنجیره تامن خون  انتخاب بهترین ترکیب تکنولوژی ها و از مشکلات عملیاتی میتوان به دشواری تخصیص اهداکنندگان به روش های جمع آوری اشاره کرد. این تصمیمات پیچیده میباشند زیرا باید فاکتورهای زیادی در نظر گرفته شود، از جمله تقاضای تصادفی، سازگاری گروه های خونی، در دسترس بودن اهدا کننده، نسبت گروه های خونی در جمعیت اهدا کننده و گیرنده، هزینه های ثابت و متغیر و هزینه های فرایند.  استفاده از پیش بینی های تقاضای قطعی کافی نیست به همین دلیل نیاز به یک تصمیم استوار میباشد که باید عدم قطعیت و تغییرپذیری در تقاضا و عرضه را در نظر بگیرد. در این مقاله یک مدل برنامه ریزی خطی عدد صحیح تصادفی چند هدفه برای پشتیبانی از چنین تصمیماتی ارائه شده است. مدل تقاضا را تصادفی در نظر گرفته است و به دنبال بهینه سازی دو هدف است: مجموع هزینه ها و تعداد اهدا کنندگان مورد نیاز. برای حل این مسئله، ترکیب جدیدی از الگوریتم نمونه متوسط تقریبی (SAA) ​​و الگوریتم  اپسیلون-محدودیت استفاده شده است. این رویکرد با استفاده از داده های واقعی از بوگوتا، کلمبیا نشان داده شده است.

واژه‌های کلیدی: تحقیق در عملیات در سیستم سلامت، زنجیره تأمین خون، جداسازی خون، افرزیس، برنامه ریزی تصادفی، برنامه ریزی چند هدفه

مقدمه

زنجیره تامین خون شامل فرآیندهای جمع آوری، آزمایش، پردازش و توزیع خون و فرآورده های خونی، از اهداکننده تا گیرنده میباشد. افزایش تقاضا برای فرآورده های خونی و همچنین کاهش جمعیت اهدا کنندگان، تصمیم گیری را در مورد زنجیره تامین خون به چالش می کشد. از طرف دیگر، محدودیت ماندگاری، چند فرآورده بودن خون، سازگاری و نسبت خون باعث می شود مشکل پیچیده تر شود و مجموعه روش های مناسب را محدود کند.

زنجیره تامین خون با شکل های مختلف در کشورهای توسعه یافته و در حال توسعه یافت می شود. کشورهای توسعه یافته تمایل به داشتن سیستم های متمرکز دارند، در حالی که، در کشورهای در حال توسعه  این سیستم ها اغلب غیرمتمرکز هستند. تفاوت مهم دیگر بین کشورهای توسعه یافته و در حال توسعه در دسترس بودن منابع است. براساس آمار سازمان بهداشت جهانی، میزان اهدا خون در کشورهای با درآمد بالا 36.8 اهدا کننده در هر 1000 جمعیت است  در حالی که در کشورهای با درآمد متوسط ​​و کم درآمد به ترتیب 11.7 و 3.9 اهداکننده برای هر 1000 جمعیت است. از این رو، مدیریت زنجیره تامین خون به طور کلی چالش برانگیز است. با این حال، ویژگی هایی از قبیل منابع اقتصادی، رفتار اهدا کنندگان و عدم تمرکز سیستم، این نوع تصمیمات را در کشورهای در حال توسعه حتی چالش برانگیزتر کرده است. یکی از شکاف های شناسایی شده در بررسی ادبیات زنجیره تامین خون، تصمیمات مربوط به راه کارهای تحقق تقاضا با توجه به اهدای خون  کامل و آفرزیس میباشد که به ندرت به طور کلی مورد مطالعه قرار گرفته است.

این مقاله به بررسی مسئله در دو مرحله پرداخته است:  در مرحله اول، مدل ارائه شده در این مقاله شامل چندین ویژگی است که در تحقیقات قبلی در مدل های کمی برای زنجیره تامین خون مورد توجه قرار نگرفته است، به عنوان مثال، ترکیب عدم قطعیت و چند هدفه بودن به طور همزمان. علاوه بر این، این مدل شامل جنبه های دیگری است که بندرت در ادبیات زنجیره تامین خون مانند در نظر گرفتن چندین روش برای جمع آوری و چندین فراورده بودن خون به طور همزمان مورد توجه قرار داده است. با توجه به تقاضای تصادفی سالانه برای محصولات خونی، این مدل از تصمیمات استراتژیک مانند انتخاب تکنولوژی و تخصیص اهداکنندگان به روش های جمع اوری و استفاده از محصولات جایگزین به منظور پاسخگویی به تقاضا و در ضمن به حداقل رساندن هزینه و تعداد اهدا کنندگان مورد نیاز پشتیبانی می کند.

 در مرحله دوم، برای مقابله با عدم قطعیت و چندین هدفه بودن مدل، روشی جدید ارائه داده است که دو رویکرد دیگر را شامل می شود، نمونه متوسط تقریبی ​​(SAA) و الگوریتم  اپسیلون-محدودیت. مدل و روش پیشنهادی با استفاده از داده های واقعی در حوزه عمومی از بوگوتا، کلمبیا ارزیابی می شود

نوآوری:

·            روشی جدید برای مسئله بهینه سازی چند هدفه تصادفی

·            ارزیابی شکاف بهینه برای هر جواب غیر کارا

·            توجه به چند ویژگی مهم زنجیره تامین خون

·            بحث در مورد روش های مختلف راه حل برای مسئله SAA

شرح مسئله

متداول ترین روش جمع آوری، اهدا خون کامل نام دارد­، که شامل استخراج تقریبا 450 میلی لیتر خون از اهدا کننده است. انواع مختلفی از کیسه­های جمع آوری وجود دارد که هرکدام محصولات خونی مختلفی دارند. کل خون سانتریفیوژ می­شود و بسته به نوع کیسه­ای که برای جمع آوری مورد استفاده قرار می­گیرد، به اجزای مختلف مانند گلبول های قرمز، پلاکت­ها، انجماد و پلاسما تقسیم می­شود. یک روش جمع آوری جایگزین، افرزیس است که مستقیماً یک جزء خون واحد را از یک اهدا کننده خارج می­کند، به طور قابل توجهی کارآمدتر از روش خون کامل میباشد. به عنوان مثال، دو واحد گلبول قرمز می تواند از یک اهدا کننده با استفاده از روش افرزیس بدست آید، در حالی که خون کامل فقط یک واحد دارد. با این حال، افرزیس نیز معایبی مانند گرانی تجهیزات، رعایت ویژه فرد برای سطح هموگلوبین و ... را نیز دارد

جدول زیر پنج فرآیند متداول و کمیت محصولات حاصل از اختصاص یک اهدا کننده به هر فرآیند را نشان می دهد. مقادیر در واحد انتقال استاندارد نشان داده شده است.

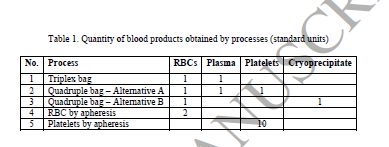
از دیگر ویژگی های خون که باعث پیچیده تر شدن زنجیره تامین خون میشود، امکان استفاده از محصولات جایگزین است. به طور کلی، گروه های خونی در چهار گروه (A, B, AB, O) تعریف می شود که هر کدام توسط فاکتور رزوس (مثبت یا منفی) تقسیم می شوند. سازگاری بین این هشت نوع خون بسته به کالایی که باید مورد استفاده قرار گیرد متفاوت است. علاوه بر این، سازگاری های انتقال خون نیز می تواند با توجه به عواملی مانند ترجیح پزشک، درمان های خاص پزشکی و در دسترس بودن متفاوت باشد.

هدف از مدل ارائه شده در این مقاله، دستیابی به مجموعه ای از جواب ها میباشد؛ که با توجه به تقاضای غیر قطعی، هم هزینه و هم تعداد اهدا کنندگان مورد نیاز را بهینه می کند. این مدل با یک مطالعه موردی نشان داده شده است که از داده های واقعی در مورد عرضه و تقاضا برای اهداکنندگان خون در طی یک سال در بوگوتا، کلمبیا استفاده کرده است.

مدل ریاضی:

مدل برنامه ریزی خطی عدد صحیح ارائه شده در این بخش، به دنبال بهینه کردن دو تابع هدف میباشد. کمینه کردن کل هزینه های جمع آوری و تعداد اهدا کنندگان. متغیرهای تصمیم گیری تعداد ماشین هایی است که باید خریداری شود، تعداد اهدا کنندگان مورد نیاز، استراتژی جمع آوری / تولید و خط مشی استفاده از محصولات جایگزین. سایر ویژگیهای خاص زنجیره تامین خون مانند تناسب گروه های خونی، چندین فرآورده بودن خون استفاده از محصولات سازگار و روش های مختلف جمع آوری، یا به عنوان محدودیت مدل سازی شده اند یا در تعریف متغیرهای تصمیم گیری گنجانده شده اند.

مدل قطعی:

تابع هدف اول (1): بیانگر کل هزینه سالانه، تأمین تقاضا برای محصولات خونی، از جمله کلیه هزینه های متغیر و ثابت است.

 تابع هدف دوم (2): تعداد کل اهدا کنندگان مورد نیاز برای پاسخگویی به تقاضا را با توجه به انواع خون و فرایندها محاسبه می کند.

 محدودیت (3): تضمین ارضای تقاضا برای هر محصول

محدودیت ها (4): مقدار محصول موجود را به عنوان تابعی از تعداد اهدا کنندگان تعریف می کند.

 محدودیت (5) اطمینان می دهد که تناسب هر گروه خونی در جمعیت مورد مطالعه حفظ می شود.

 محدودیت های ظرفیت (6) میزان دسترسی هر منبع را با توجه به تعداد واحد تجهیزات برای هر تکنولوژی تعریف می کند.

 محدودیت های (7) تعداد اهداکنندگانی را که می توانند به فرآیند تولید RBC ها از طریق روش افرزیس قرار گیرند، محدود می کند، زیرا تنها بخشی از جمعیت واجد شرایط برای اهدا با این روش هستند.

رقابت بین توابع هدف (1) و (2) به وجود می آید زیرا روش های مختلف زیادی برای اختصاص اهدا کنندگان به روش جمع آوری وجود دارد که از نظر هزینه و کمیت محصولات به دست آمده متفاوت هستند. مقادیر هر عملکرد هدف در جدول 2 آورده شده است و از این مقادیر برای سه مورد استفاده شده است.

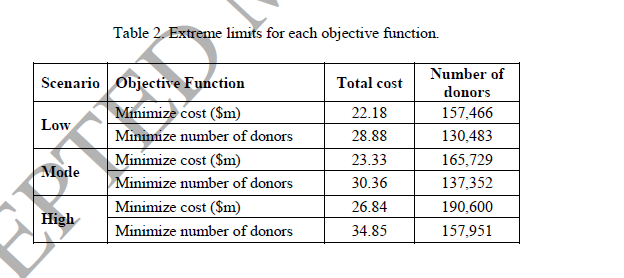
تدوین مسئله به عنوان یک مدل بهینه سازی تصادفی دو مرحله ای

در واقعیت، تقاضا شناخته نشده است، اما تصمیم گیری در مورد تعداد ماشین های که برای هر نوع تکنولوژی باید خریداری شود، باید در ابتدا  افق برنامه ریزی، قبل از تحقق تقاضا اتخاذ شود. چالش تصمیم گیری های خوب در این مرحله است که ماهیت تصادفی تقاضا را در نظر می گیرد. اطلاعات مربوط به تعداد اهداکنندگان مورد نیاز هر فرآیند و گروه خونی پس از آشکارسازی عدم قطعیت مشخص می شود.

به منظور در نظر گرفتن این عدم قطعیت، مدل قطعی  را می توان به عنوان یک مدل برنامه ریزی خطی تصادفی دو مرحله ای بازنویسی کرد. که در مرحله اول این مسئله، به عنوان یک مسئله بهینه سازی چند هدفی تدوین شده است که در آن  همزمان به کمینه کردن کل هزینه های مورد انتظار و هم حداکثر تعداد اهدا کنندگان را که در مرحله دوم مجاز هستند پرداخته است. به مدل یک متغیر تصمیم جدید اضافه شده است تا نمایانگر این حد بالایی در تعداد اهدا کنندگان باشد

تابع هدف اول : کل هزینه مورد انتظار را نشان می دهد. متغیرهای تصمیم گیری q و تعداد ماشینهای y_t  برای هر نوع فناوری t  است که باید خریداری شوند. بخش دوم تابع هدف، مقدار مطلوب مسئله بهینه‌سازی تک هدفه تصادفی مرحله دوم را مشخص می کند، که ξ (یک بردار تصادفی) نشان دهنده تصادفی بودن تقاضا است.

تابع هدف دوم: q را به حداقل می رساند متغیر q در مسئله مرحله دوم به عنوان حد بالایی در تعداد اهدا کنندگان مورد نیاز تعیین شده است.

بخش دوم تابع هدف اول  که در مرحله دوم به حداقل می رسد به شرح زیر نوشته میشود:

محدودیتهای (4) - (7) و نسخه تصادفی محدودیت ها:

تابع هدف (12) متغیر هزینه جمع آوری و مجازات کمبود را محاسبه می کند. مرحله اول پیدا کردن مقدار y و q  میباشد. مرحله دوم بیانگر تصمیماتی است که با توجه به تحقق تقاضا قابل تغییر است.  محدودیت (13) تعداد اهداکنندگان را با استفاده از حد بالایی q محدود می کند که در مرحله اول یک متغیر تصمیم گیری بود.

عدم قطعیت در زنجیره تامین خون عمدتاً به دو منبع، تقاضا برای محصولات و عرضه اهدا کنندگان مرتبط است. تقاضا برای محصولات بستگی به عوامل بسیاری از جمله جراحی، معالجه بالینی، شرایط اضطراری و بلایای مختلف دارد. از طرف دیگر، اهداء خون فرایندی داوطلبانه است که عمدتا به انگیزه نوع دوستانه بستگی دارد. عدم قطعیت در عرضه اهدا کنندگان به صراحت مدل نمی شود. با این حال، می توانیم تأیید کنیم که تعداد هدف مطلوب اهداکنندگان در نتایج همیشه کمتر از تعداد واقعی اهداکنندگان مشاهده شده در داده های مورد بررسی است. همچنین لازم به ذکر است که مدیران بانک خون می توانند در صورت لزوم از استراتژی های مختلفی برای افزایش جمع آوری خون استفاده کنند. این راهکارها شامل تبلیغات هدفمند برای گروه های خونی خاص، کمپین های ویژه در مکان های محبوب و ... است.

رویکرد راه حل

در این بخش برای حل مدل ارائه شده، یک رویکرد جدید ارائه شده است که ترکیبی از روش SAA و الگوریتم اپسیلون  محدودیت است. ایده کلی حل یک مسئله  SAA برای هر مقدار epsilon است. مرز پارتو از مقدار اختصاصی یک هدف و مقدار مورد انتظار از هدف دیگر تشکیل شده است. مراحل این رویکرد یکپارچه در زیر شرح داده شده است.

الگوریتم اپسیلون محدودیت:

تبدیل یک مسئله چند هدفه به یک مسئله تک هدفه. برای انجام این کار، تصمیم گیرنده باید یک تابع هدف را انتخاب کند تا به عنوان هدف باقی بماند و تابع هدف های دیگر را به عنوان محدودیت هایی که توسط مجموعه ای از پارامترها به نام اپسیلون محدود می شود، تعیین کند. این پارامترها به طور جداگانه برای هر هدف که به یک محدودیت تبدیل می شوند، تعریف می شوند. در مرحله اول، تابع هدف دوم f (q) به یک محدودیت تبدیل می شود و برابر با یک پارامتر ε همانطور که در معادله (15) نشان داده شده است تنظیم می شود:

با توجه به این تغییرات، مسئله مرحله اول (چند هدفه) می تواند به شرح زیر بازنویسی شود:

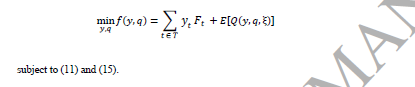
مرحله اول با به حداقل رساندن هزینه های کل( که با استفاده از متغیر مازاد اضافی w  نشان داده است) و برای آن یک ضریب b در نظر گرفته شده است:

و محدودیت 13 به شکل زیر بازنویسی میشود:

پس مسئله مرحله دوم می تواند به شرح زیر بازنویسی کرد:

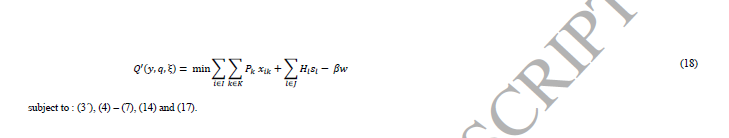
نمونه میانگین تقریبی (SAA)

روش SAA با استفاده از نمونه‌گیری از عدم قطعیت سر و کار دارد. از این رو می توان مقدار Q` از تابع هدف مرحله دوم را با در نظر گرفتن میانگین مقادیر نمونه های اندازه N محاسبه کرد. در این حالت حاصل مدل، عدد صحیح و خطی است. در واقع در این بخش به شمارش تعداد دفعاتی که نقض محدودیت اتفاق میفتد میپردازد.

بنابراین می توان کل مسئله را به شرح زیر بیان کرد:

روش کامل SAA  به شرح زیر است:

گام 1:

از هر اندازه N، نمونه مستقل M تولید کنید و برای هر نمونه، SAA مربوطه را حل کنید.

گام 2:

شاخص های آماری زیر را محاسبه کنید:

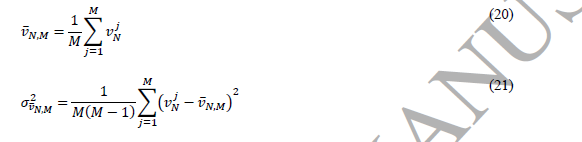
گام 3:

با استفاده از عبارت زیر مقدار واقعی  f را تخمین بزنید:

واریانس را با توجه به اندازه N` محاسبه میشود. ( دراین گام از N`  انتظار میرود که به میزان قابل توجهی از اندازه N که در گام1 استفاده شده است، بزرگتر باشد.)

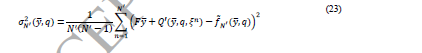
گام 4:

برآوردگر بهینه را بر اساس نتایج حاصل از مراحل 2 و 3 محاسبه کنید

واریانس شکاف بهینه را با استفاده از عبارت زیر تخمین بزنید:

بسته به ماهیت متغیرها و اندازه مسئله، مسئله SAA ارائه شده در معادله (19) می تواند چالش برانگیز باشد. از آنجا که استفاده از این رویکرد برای یک مسئله چند، به معنی حل چندین مسئله SAA برای مقادیر مختلف ξ است، زمان رسیدن به جواب برای هر یک از مسئله SAA بسیار مهم است. بنابراین، رویکرد رسیدن به جواب کارآمد برای مسئله SAA باید با دقت انتخاب شود.

ادغام رویکردهای SAA و اپسیلون محدودیت:

هنگامی که مدل چند هدفه به یک مسئله بهینه سازی تک هدف تبدیل شده است و همچنین یک روش حل مناسب برای مسئله SAA انتخاب شده باشد. رویکرد یکپارچه می تواند پیش رود.

الگوریتم پیشنهادی:

در اینجا δ مقدار گام (افزایش) را برای ξ نشان می دهد،  lb ، ub به ترتیب حد پایین و بالایی برای هستند.

نتیجه گیری و تحقیقات بیشتر

تصمیم گیری در محیط های غیر قطعی یک کار پیچیده است. روش مورد استفاده برای تولید جواب های استوار  برای مسئله  با پارامترهای تصادفی، هم به ویژگی های مسئله و هم به منابع موجود بستگی دارد. از آنجا که مدل ارائه شده در این مقاله خطی است و حل نسخه قطعی سازی آسان میباشد، در این مقاله یک روش یکپارچه را با استفاده از روش SAA همراه با محدودیت اپسیلون افزوده توسعه داده شده است.

 این رویکرد جواب استواری تولید میکند که ماهیت تصادفی تقاضا را در نظر می گیرد و همچنین تضمین می کند ویژگی هایی مانند تناسب و سازگاری برآورده شوند. زنجیره تامین خون به طور گسترده مورد مطالعه قرار گرفته است، اما تحقیقات قبلی عمدتاً بر توسعه سیاست های موجودی متمرکز شده است. مدل ارائه شده در این مقاله به مراحل تصمیم گیری می پردازد که توجه کمتری به آن داشته اند، یعنی جمع آوری و تولید.  علاوه بر این، این مدل به جای تمرکز بر روی یک  محصول، فرآورده های خون را در نظر می گیرد، زیرا فرآیندهای کسری( جداسازی) همیشه بیش از یک محصول را تولید می کنند.

 در عمل، استراتژی جمع آوری مطلوب به عوامل مختلفی از جمله ساختار تقاضا، ترجیحات پزشک، روش های مختلف جمع آوری و حداکثر هزینه مجاز بستگی دارد. در این مقاله، رابطه بین تعداد اهدا کنندگان مورد نیاز و هزینه ارائه شده است. در واقعیت، اتخاذ تصمیمات بهینه با توجه به جنبه های زنجیره تامین خون مانند سازگاری و تناسب، بدون استفاده از روش های پیشرفته تصمیم گیری، غیرممکن است. مدل ارائه شده در این مقاله  به راحتی می تواند توسط مراکز خونی برای برنامه ریزی استراتژی جمع آوری آنها مورد استفاده قرار گیرد، زیرا داده های لازم معمولاً در سیستم های اطلاعاتی مرکز خون در دسترس است. این مدل استفاده از محصولات جایگزین را فرض می کند، اما با تغییر پارامترهای سازگاری می توان به راحتی قوانین جایگزینی را اعمال کرد.

روش های زیادی وجود دارد که می توان این مدل را گسترش داد. در این مقاله، فقط متداول ترین فرآورده های خونی و فرایندهای تولید را در نظر گرفته است. که میتوان دیگر فرآورده های خون و دیگر روش های جمع اوری خون را نیز در نظر گرفت و مدل را گسترش داد. در نظر گرفتن درج تصمیماتی برای خرید محصولات خونی از تأمین کنندگان خارجی در این مدل مجاز است. می توان بهترین روش برای تأمین تقاضا، از جمله منابع داخلی و خارجی تأمین را مطالعه کرد. سرانجام، گنجاندن انواع مختلف تقاضا و ترجیحات بر سازگاری ها نیز می تواند به راحتی مدل شود.