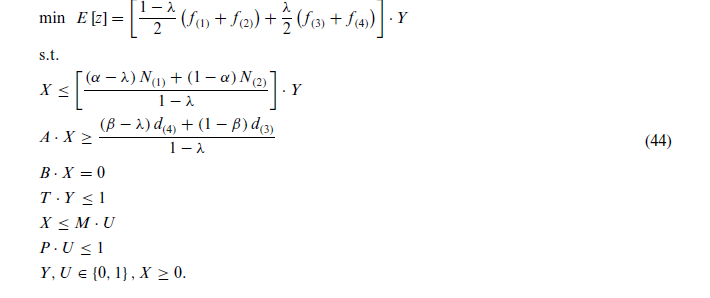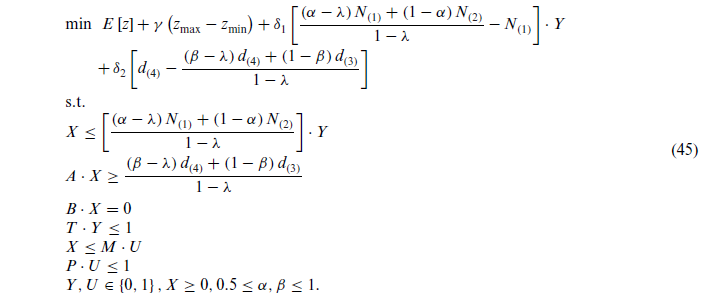طراحی شبکه خدمات درمانی: یک رویکرد استوار امکانی ( مقاله یازدهم)

چکیده:

در این مقاله یک مدل برنامه‌ریزی غیرخطی عدد صحیح دو هدفه (BO-MINLP) به‌منظور طراحی شبکه خدمات سلامت سه سطحی سلسله مراتبی بررسی می‌شود. هدف مدل کمینه‌سازی هزینه کل استقرار تسهیلات و مسافت وزن‌دار بین مناطق بیمار و مراکز درمانی می‌باشد. برای مقابله با عدم‌قطعیت پارامترها, چهار نوع مدل ترکیبی برنامه‌ریزی امکانی استوار (HRPP) معرفی می‌شود. در نهایت، یک مطالعه موردی برا ی نشان دادن عملکرد وکابرد مدل‌های، (HRPP) در عمل ارائه می‌شود.

کلید واژه‌ها: خدمات درمانی، تخصیص و مکان‌یابی سلسله مراتبی، سیستم ارجاع، برنامه‌ریزی دو هدفه، برنامه‌ریزی امکانی استوار

   مقدمه:

پیش نیاز اصلی سیستم‌های بهداشتی برای دستیابی به هدف نهایی "کاهش نابرابری درمانی" است که به معنی ارائه خدمات درمانی به همه مردم است. از این رو، طراحی شبکه خدمات درمانی یک تصمیم استراتژیک مهم است: که بر عملکرد سیستم ملی سلامت مرتبط است. مکان‌یابی مراکز ارائه خدمات، نوع خدمات و ظرفیت خدمات ارائه شده، تخصیص مناطق جغرافیایی به ارائه‌دهندگان خدمات بهداشتی و درمانی  و طراحی سیستم ارجاع به صورت سلسله مراتبی برخی از تصمیمات اصلی استراتژیک است که باید هنگام ایجاد شبکه خدمات درمانی اتخاذ شود. بدیهی است که شبکه های بهداشتی بسیار گسترده‌تر از 30 سال پیش هستند، اما هنوز بسیاری از گروه‌ها به درستی پوشش داده نشده‌اند .در نتیجه، گسترش عادلانه شبکه های خدمات درمانی امروزه نیز اولویت دارد.

مکان‌یابی تسهیلات می‌تواند به عنوان یک حوزه تحقیقاتی قدیمی در نظر گرفته شود که برنامه‌های آن هنوز هم مورد توجه قرار می‌گیرند. در این شاخه تحقیقاتی مربوط به مکان‌یابی یا استقرار حداقل یک تسهیلات بین تسهیلات موجود به منظور  بهینه‌سازی (کمینه یا بیشیه سازی) حداقل یک تابع هدف شامل: هزینه، سود، درآمد، فاصله سفر، خدمات، زمان انتظار، پوشش و سهام بازار می‌باشد.

نوآوری

·            توسعه مدل برنامه‌ریزی غیرخطی عدد صحیح دو هدف BO-MINLP)) به‌منظور طراحی شبکه سیستم های سلامت سه سطحی سلسله مراتبی.  این مدل تعدادی از تصمیمات حیاتی شامل مکان‌یابی بری ارائه‌دهندگان خدمات سلامت در سطوح مختلف، ظرفیت تأسیسات امکانات، تخصیص مناطق به PHC ، الگوی ارجاع بیماران در سراسر شبکه و نمونه کارها خدمات درمانی ویژه در DHC را به طور همزمان محاسبه می‌کند.

·            ارائه چهار نوع مدل ترکیبی برنامه ریزی امکانی استوار(HRPP) برای مقابله با عدم قطعیت شناختی پارامترها.

·            ارائه یک مطالعه موردی واقعی در شهر تهران برا ی نشان دادن عملکرد و کابرد مدل پیشنهادی.

توضیحات و فرمول مسئله

مساله به یک زنجیره تامین سلسله مراتبی سه سطحی ( (3-LHSNDشامل مناطق بیمار (کاربران خدمات بهداشتی)،  پزشک خانواده (PHC)، که خدمات بهداشتی عمومی و پیش‌گیری کننده را ارائه می‌دهند و به عنوان نقاط ورودی به سیستم سلامت می باشد، کلینیک‌ها(RHC)   و بیمارستان‌های تخصصیDHC)) که خدمات درمانی ویژه‌ای را به بیماران ارائه می‌دهند.  تصمیمات اصلی که توسط مدل پیشنهادی اتخاذ می‌شود شامل مکان و ظرفیت امکانات مراقبت‌های بهداشتی در سطوح مختلف، پکیج خدمات درمانی ویژه در هرDHC ، تخصیص کاربری مناسبPHCها ، ارجاع از PHC به RHC ها و از RHC ها به DHC و گردش بیماران در کل شبکه می‌باشد. شکل 1 ساختار شبکه سیستم سلامت مربوط را نشان می‌دهد.

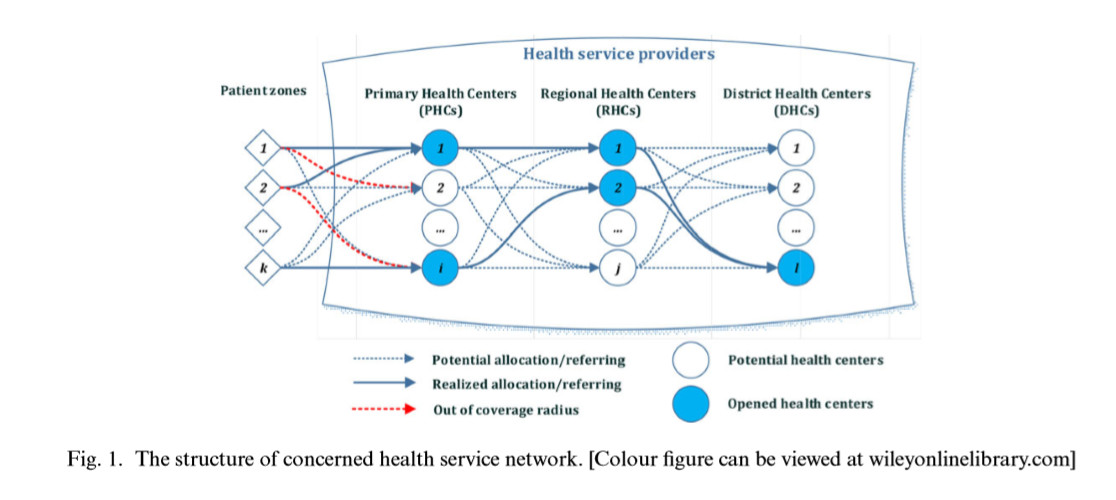
مفروضات اصلی مورد استفاده برای فرمولاسیون مساله به شرح زیر توصیف می‌شود:

·            بیماران به تعدادی از مناطق بیمار دسته‌بندی می‌شوند که در آن اکثریت جمعیت هر منطقه بیمار در حوالی مرکز مربوطه سکونت دارند. بر این اساس، کلیه مکان‌های کاندیدایی در وسط مناطق بیمار قرار گرفته است.

·            تقاضای کلیه مراکز درمانی مستقر (PHC ، RHC و DHC  ) باید کاملاً برآورده شود.

·            هیچ تسهیلات از پیش تعیین شده وجود ندارد و قرار است همه تسهیلات تازه تاسیس شود. با این حال، اگر امکان تسهیلاتی از قبل وجود داشته باشد متغیر باینری مربوطه 1 می‌گیرد از این رو، مدل پیشنهادی می‌تواند به سادگی برای گسترش شبکه مورد استفاده قرار گیرد.

·            حداکثر یک تسهیل در هر سطح از شبکه در هر مکان کاندیدی می تواند مستقر شود. با این وجود، صرفه جویی در هزینه تسهیلات دو منظوره در یک مکان وجود دارد. لازم به ذکر است که منطقه جغرافیایی مورد بررسی به تعدادی از مناطق کوچک (به عنوان مثال ، مناطق بیمار) تقسیم می‌شود به گونه ای که هر منطقه حداکثر به یک مرکز درمانی در هر سطح از شبکه احتیاج دارد.

·            کلیه تسهیلات دارای ظرفیت هستند و هر مرکز در یکی از سطح ظرفیت موجود قابل افتتاح است. علاوه بر این، ظرفیت PHC و RHC با تعداد مراجعات بیماران مطابقت دارد که می‌تواند در یک افق زمانی معین توسط پزشک معالج پاسخ دهد در حالی که ظرفیت خدمات ویژه در هر DHC را تعداد تختهای مربوط به بیمارستان را مشخص می‌کند.

·            حداکثر یک مکان  کاندید برای ایجاد تأسیسات جدید در هر منطقه بیمار وجود دارد.

·            حداکثر تقاضای هر منطقه بیمار در هر سطح کمتر از بیشنه ظرفیت PHC ، RHC و DHC است.

·            در سطحDHC ، خدمات بهداشتی ویژه در گروه‌های مختلف تقسیم می‌شوند و هر DHC می‌تواند بسته کاملی از این خدمات تخصصی را ارائه دهد.

·            کل تقاضای یک منطقه بیمار فقط با یک PHC برآورده می شود، هر PHC بیماران را دقیقاً به یک RHC ارجاع می‌دهد و به طور مشابه، هر RHC بیماران را فقط به یک DHC برای هر گروه خدمات تخصصی ارجاع می‌دهد.

·            هزینه افتتاح یک تسهیل جدید در هر مکان کاندید شامل هزینه‌های ثابت ساخت و هزینه‌های راه اندازی مثل  هزینه‌های عملیاتی در افق برنامه‌ریزی می‌باشد.

·            شعاع پوشش فقط برای PHC ها در نظر گرفته می شود زیرا ممکن است بیماران حتی درصورت مسافت نسبتاً طولانی از محل زندگی خود به مراکز سطح بالاتر (یعنی کلینیک‌ها یا بیمارستان‌ها) مراجعه کنند.

ابتدا مسئله با داده‌های قطعی مدل سازی شده است و سپس مدل‌های برنامه‌ریزی استوار امکانی ارئه شده است که داده‌های غیردقیق (یعنی احتمالی) را بررسی می‌کند.

 مدل پیشنهادی BO-MINLP :

تابع  هدف (1) شامل هزینه های ثابت افتتاح مراکز  برای استقرار PHC ، RHC  و DHC است. صرفه جویی‌های هزینه‌ای در تسهیلات دو منظوره از هزینه کل کم می‌شود. تابع هدف (2) به ترتیب شامل سه بخش، از جمله زمان کل سفر مناطق بیمار به PHC ،  RHC و DHC می‌باشد.

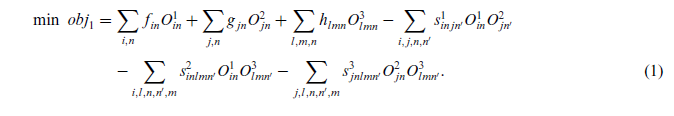
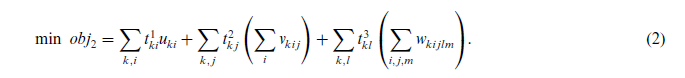
بدیهی است که دو هدف متناقض هستند. در واقع، ایجاد مراکز درمانی کمتر در شبکه بهداشت, منجر به کاهش هزینه‌ها می‌شود، در حالی که دسترسی عمومی به شبکه سلامت کاهش می‌یابد (یعنی کل زمان سفر بیماران افزایش می‌یابد) و بالعکس. با این حال، این اهداف از ضرورت یکسانی در همه‌ی موارد برخوردار نیستند. در سیستم‌های سلامت بخش خصوصی تصمیم‌گیرنده (DM) عمدتاً بر روی به حداقل رساندن هزینه و به حداکثر رساندن سود تمرکز می‌کند، در حالی که در بخش عمومی، حداکثرسازی دسترسی عمومی هدف اصلی شبکه بهداشت می‌باشد. این تضاد با استفاده از یک روش تصمیم‌گیری چند هدفه در بخش های بعدی مورد بحث قرار گرفته است. محدودیت های  (3) - (5) تضمین می‌کنند که کل جریان دریافتی از سطح قبلی نمی تواند از ظرفیت خدمات سطح مربوط تجاوز کند.

معادلات (6) - (8) به‌ترتیب رضایت کامل تقاضا PHC ،  RHCو DHC را تضمین می‌کند.

معادلات (9) - (11) نشان می‌دهد که هر مرکز بهداشتی کاندیدا می‌تواند در یک سطح از خدمات قابل دسترس تأسیس شود.

معادله (12) نشان می‌دهد که یک جریان از بیماران منطقه  kبه PHC_i   وجود خواهد داشت، اگر این PHC قبلاً به این منطقه بیمار اختصاص یافته باشد و اگر این منطقه بیمار در شعاع پوشش آن PHC قرار داشته باشد . معادلات (13) و (14) تضمین  می کنند که فقط یک جریان به RHC یا DHC می تواند رخ دهد اگر و فقط اگر آنها از طریق الگوی تخصیص انتخاب شده با هم در ارتباط باشند.

که در معادلات فوق به جای M¹ ، M² و M³_m عبارات زیر را قرار داده می‌شود:

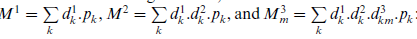
معادلات (15) - (17) سیستم استاندارد ارجاع درمانی را تضمین می‌کند.

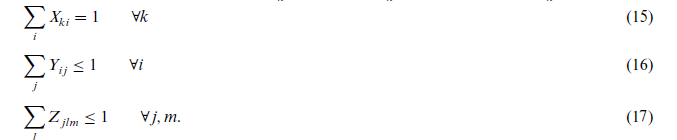
محدودیت (18) نشان می‌دهد که اگر یک PHC در منطقه بیمار معین افتتاح شود، ساکنان این منطقه توسط آن PHC خدمت دریافت می‌کنند. محدودیت‌های (19) و (20) نشان می‌دهند که اگر دو مرکز بهداشتی متعلق به دو سطح مختلف متوالی شبکه بهداشت و درمان در همان محل کاندیدایی افتتاح شود، در همان مرحله مرکز سطح پایین به مرکز سطح بالا اختصاص می‌یابد.

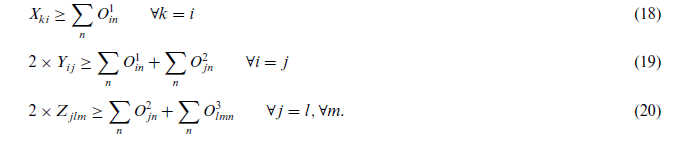
سرانجام ، معادلات (21) و (22) محدودیت‌های باینری و غیرمنفی را بر روی متغیرهای تصمیم مربوطه اعمال می‌کنند.

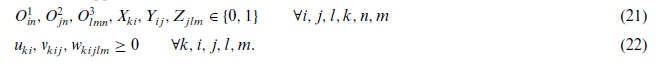
بررسی داده ای غیرقطعی

بیشتر پارامترهای موجود در مساله طراحی شبکه سلامت مورد بررسی (به عنوان مثال داده‌های تقاضا برای خدمات بهداشتی در سطوح مختلف شبکه، هزینه‌های افتتاح تاسیسات بهداشتی و زمان سفر بیمار) با درجه بالایی از عدم اطمینان در واقعیت آمیخته می‌شوند که این به دلیل  ماهیت پویا مسئله (به‌عنوان مثال، نوسانات ممکن در مقادیر پارامترها در افق بلند مدت) می‌باشد. در چنین شرایطی، استواری راه‌حل نهایی از اهمیت ویژه ای برخوردار است، زیرا در مورد تصمیم‌گیری در مورد تخصیص و مکان‌یابی و تعیین ظرفیت در یک افق بلند مدت قابل تغییر نیست. با در نظر گرفتن این واقعیت ها، برای مقابله با پارامترهای غیر قطعی در مساله 3-LHSND  پیشنهادی، یک رویکرد HRPP جدید در این مقاله تدوین شده است. پس از این، برنامه‌ ریزی استوار و رویکردهای برنامه ریزی فازی به طور خلاصه معرفی می‌شوند. سپس، رویکرد HRPP پیشنهادی ارائه می‌شود، که مبتنی بر جدیدترین اندازه فازی موجود در ادبیات است (یعنی اندازه Me ).

برنامه‌ریزی استوار

در اکثر مسائل در سطح استراتژیک، DM ها تمایل دارند یک تصمیم پایدار بگیرند که هم از نظر شدنی بودن و هم بهینگی دارای استواری باشد. استواری شدنی بودن بدان معنی است که راه حل باید برای تقریباً همه مقادیر ممکن پارامترهای غیر قطعی امکان پذیر باشد و استواری بهینگی به معنای این است که مقدار تابع هدف باید نزدیک به مقدار ایده ال باشد و یا حداقل انحراف را از مقدار ایده ال برای (تقریبا) همه مقادیر ممکن پارامترهای غیر قطعی داشته باشد. رویکردهای برنامه‌ریزی استوار را می‌توان به سه گروه طبقه بندی کرد : الف) رویکرد بدبینانه سخت، (ب) رویکرد بدبینانه نرم  و (ج) رویکرد واقع بینانه.  در روش بدبینانه سخت،  فرض می‌شود که همه پارامترهای غیرقطعی بدترین خود را بگیرند، که در بین این سه رویکرد به عنوان بدبینانه ترین حالت (یعنی محافظه کارانه) شناخته می‌شود. نقطه ضعف اصلی این روش این است که روی استواری شدنی بودن متمرکز شده و بنابراین کمترین استواری بهینگی را به دست می‌آورد. بنابراین به نظر می‌رسد فقط برای شرایط اضطراری و نظامی مناسب است. در عوض، این روش نیاز به اطلاعات اضافی درباره توزیع امکان یا احتمال پارامترهای غیرقطعی  را از بین می برد. رویکرد بدبینانه نرم نسبتاً منعطف‌تر از رویکرد اول است زیرا سعی می‌کند بدترین مقدار تابع هدف  را کمینه کند، در حالی که تمامی محدودیت‌ها را در بدترین حالت خود برآورده نمی‌کند. سرانجام، رویکرد واقع‌بینانه تلاش می‌کند بین استواری راه‌حل به‌دست آمده و هزینه استوارای تعادل برقرار می‌کند (به‌عنوان مثال، دارای منطق هزینه- منفعت  است و بنابراین برای زمینه‌های تجاری مناسب است).

برنامه ریزی ریاضی فازی

برنامه‌ریزی ریاضی فازی (FMP)قادر است به طور مناسب عدم قطعیت شناختی در داده‌ها و انعطاف‌پذیری در اهداف یا  محدودیت‌ها را کنترل کند. FMP را می توان به دو دسته بندی اصلی طبقه بندی کرد: (الف) برنامه‌ریزی امکانی (pp). ب) برنامه‌ریزی منعطف. برنامه ریزی امکانی برای مواجهه با عدم قطعیت شناختی داده ها به کار برده می‌شود که توزیع امکان آن با توجه به داده های موجود یا نظر  DM  و یا با کمک خبره تعیین می‌شود. برنامه‌ریزی منعطف برای مقابله با عدم قطعیت  در محدودیت (های) نرم و یا در مقدار تابع هدف به کار برده می‌شود. برنامه‌ریزی شرطی امکانی (محدودیت‌هایی با عدم قطعیت در داده ها)(PCCP),  یک روش شناخته شده PP  می باشد که برای مقابله  با  داده های امکانی در سمت راست و چپ به کار برده می شود. در این رویکرد  DM  یک حداقل درجه اطمینان (α)  را به عنوان حاشیه امنیت سطح ارضای  هر محدودیت شانس امکانی در نظر می‌گیرد. اندازه امکان (pos)  و الزام (nes ) دو اندازه شناخته شده فازی برای برآورد‌سازی چنین اطمینان هایی  در مدل‌های pccp  می‌باشد. اندازه امکان خوش‌بینانه‌ترین سطح احتمال وقوع پارامترهای امکانی را نشان می‌دهد در حالی که اندازه nes بدبینانه‌ترین نگرش DM را نشان می‌دهد.

عدد فازی ذوزنقه‌ای ξ = (r₁ , r_2, r_{3 ,}r₄ ) و  r_{1 <} r_2< r_{3 <}r₄  را در نظر بگیرید که تابع عضویت آن به صورت زیر مشخص می‌شود:

برای  α> 0.5  معادل قطعی توابع عضویت در اندازه‌های الزام و امکان به‌شرح زیر محاسبه می‌شود :

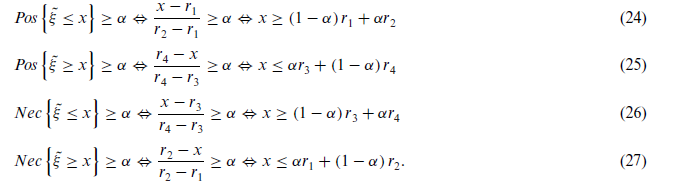
همچنین برای r₁ > 0 ارزش انتظاری اندازه‌های ذکر شده به‌صورت زیر محاسبه می‌شود:

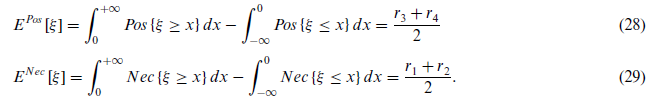
در شرایط واقعی، نگرش DM معمولاً متفاوت از چنین نگرش های افراطی است و ممکن است بین این دو افراط  خوش‌بین و بدبین تغییر کند. در این راستا ، اندازه (Cr)، که از یک نگرش بی‌طرف از DM در مورد هر دو افراط پشتیبانی می‌کند  به شرح زیر معرفی شده است:

   برای (α > 0.5) به‌صورت زیر تعریف می‌شود:

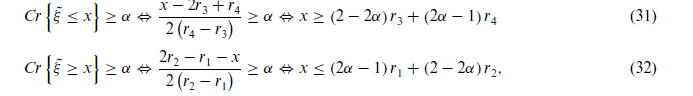
برای r₁ > 0 ارزش انتظاری اندازه باورپذیری اینگونه حساب می‌شود:

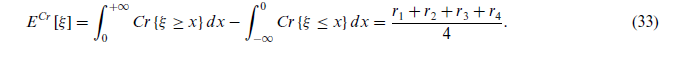
اگرچه  اندازه Cr برای جلوگیری از انتخاب خوش‌بینانه یا بدبینانه افراطی مفید است، اما DM  را مجبور می‌کند تا یک نقطه خاص  بین این دو نگرش افراطی ( میانگین امکان و الزام) را اتخاذ کنند. برای پر کردن این شکاف، Xu and Zhou (2013) یک اندازه فازی جدید ( Me measure ) معرفی کردند که از اندازه Cr  منعطف‌تر است و برای تصمیم‌گیری در شرایط واقعی در محیط فازی مناسب است. در این رویکرد، DM  می‌تواند با استفاده از ترکیبی محدب از این افراط‌ها، هر نقطه‌ای را در طیف نگرش‌های افراطی انتخاب کند:

·            وقتی λ=1  مقدار بگیرد یعنی تصمیم‌گیرنده خوش‌بینانه‌ترین نگرش را دارد در نتیجه Me = Pos  می‌شود.

·            وقتی λ=0  مقدار بگیرد یعنی تصمیم‌گیرنده  بدبینانه‌ترین نگرش را دارد در نتیجه Me = nec  می‌شود.

·            وقتی λ=0.5  مقدار بگیرد یعنی تصمیم‌گیرنده  نگرش میانه را دارد در نتیجه Me = cr  می‌شود.

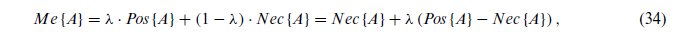
اندازه Me  به‌صورت زیر می‌باشد:

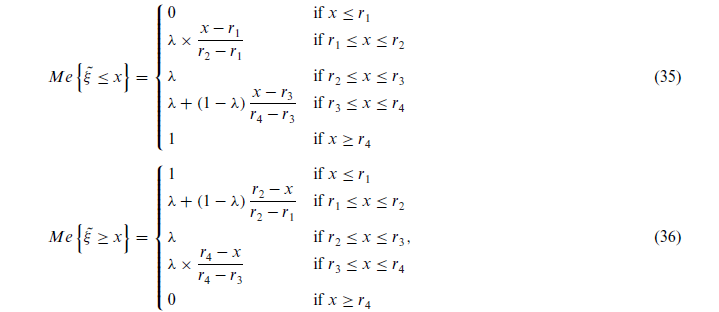
برای r₁ > 0 ارزش انتظاری اندازه  Me اینگونه حساب می‌شود:

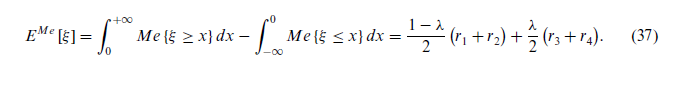
در مسائلی مانند مراقبت‌های بهداشتی و طراحی شبکه زنجیره تأمین،DM ها ترجیح می‌دهند یک رویکرد بدبینانه برای مسئله اتخاذ کنند. در این موارد، پارامتر λ ، مقداری کمتر از 0.5 را به خود اختصاص می‌دهد، که تمایل به اندازه الزام را نشان می‌دهد.

برای  ( λ > 0.5)به‌صورت زیر محاسبه می‌شود:

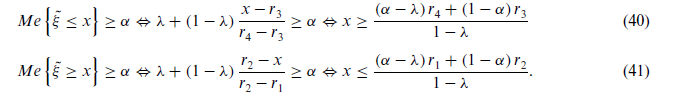
مدل پایه  (BPCCP)PCCP

به‌منظور سهولت کار، فرم فشرده مدل 3-LHSND   ( به استثنای تابع هدف دوم) به‌شرح زیر است:

بردار f  هزینه های ثابت افتتاح, ماتریس‌هایN ، A ، B ، T ، وP  ماتریس‌های ضرایب محدودیت‌ها،M  یک عدد بسیار بزرگ است. بردارهای YوU  متغیرهای باینری، بردارX  متغیرهای پیوسته مثبت را نشان می‌دهد. حال فرض کنید که بردارهایf ،  N  و d  نمایانگر هزینه‌های ثابت افتتاح، ظرفیت مراکز و تقاضا برای خدمات درمانی پارامترهای غیرقطعی باشند. برای تبدیل به مدل BPCCP ، به مدل قطعی، از عملگر ارزش انتظاری برای تبدیل تابع هدف امکانی به همتای قطعی خود استفاده می‌شود، و اندازهMe  برای مقابله با برنامه ریزی شرطی امکانی شامل پارامترهای غیرقطعی به کار برده می‌شود. در زیر، توزیع امکان ذوزنقه‌ای را برای مدل‌سازی پارامترهای غیرقطعی به کار می‌شود:

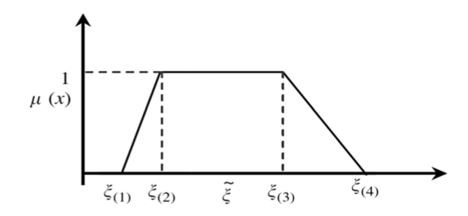
با توجه به توضیحات ذکر شده مدل BPCCP  به صورت زیر قطعی سازی می‌شود:

 با قرار دادن معادل ارزش انتظاری در تابع هدف و اندازه Me  در محدودیت‌های شانس به‌صورت زیر تعریف می‌شود:

رویکرد ترکیبی برنامه ریزی استوار امکانی ( HRPP)

اگرچه مدل  BPCCP به طور مناسبی  می تواند با پارامترهای غیرقطعی مقابله کند، اما  از آنجا که به انحراف مقدار تابع  هدف از مقدار مورد انتظار خود حساس نیست، انحراف در مقدار پارامترهای غیرقطعی در برخی از موقعیت های واقعی می‌تواند ریسک زیادی را بهDM  تحمیل کند. از این رو  استفاده از رویکردهای برنامه ریزی فازی استوار توصیه می‌شود تا هم از مزایای فازی و هم از مزایای رویکرد استوار بهره برد. در ادامه، یک رویکرد HRPP  نو معرفی می‌شود که  شامل سه رویکرد واقع گرایانه، یعنی HRPP-I ،HRPP-II ، HRPP-III و یک رویکرد سختگیرانه (یعنی HWRPP   ) می‌باشد.

مدل HRPP-I

بر پایه اندازه Me  , مدل  HRPP-I به صورت زیر تعریف می‌شود:

بخش اول، مقدار مورد انتظار z (عملکرد مورد انتظار تابع هدف) را بهبود می‌بخشد. بخش دوم استواری بهینگی جواب نهایی را با کمینه کردن فاصله بین حداکثر و حداقل مقادیر تابع هدف کنترل می‌کند، که تابع هدف حداکثر و حداقل به شرح زیر تعریف می‌شوند:

بخش سوم و چهارم، استواری شدنی بودن جواب نهایی را با مینیم کردن اختلاف مقدار سمت راست محدودیت‌ها از بدترین مقدارشان کنترل می‌کند.

مدل  HRPP-II

هنگامی که انحراف تابع  هدف از مقدار مطلوب مورد انتظار آن (یعنی بیش از حد یا زیر مقدار مورد انتظار) مهم باشد، تابع هدف HRPP-I  به فرمول زیر تغییر می‌کند و مدل HRPP-II مورد استفاده قرار می‌گیرد و محدودیت‌ها تغییر نمی‌کند (همان محدودیت‌های HRPP-I).

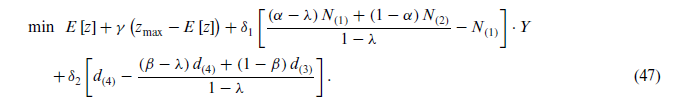
 مدل HRPP-III

اما هنگامی که DM ها نسبت به انحراف از مقدار مطلوب مورد انتظار تابع هدف حساسیت کمتری دارند به‌جای HRPP-II، تابع هدف زیر تعریف می‌شود که HRPP-III را همان محدودیت‌هایی مانند HRPP-I تشکیل می‌دهد.

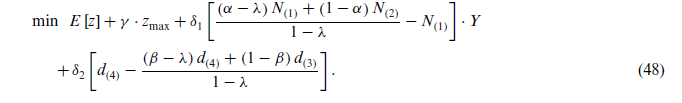
از طرف دیگر، در رویکرد بدبینانه سخت، راه‌حل به‌دست آمده باید حداکثر استواری شدنی بودن را داشته باشد، در حالی که DM  تلاش می‌کند تا بدترین مقدار تابع هدف را نسبت به همه حالات ممکن پارامترهای غیرقطعی بهبود بخشد.

 مدل‌سازی HWRPP

بنابراین مدل‌سازی رویکرد HWRPP  به‌صورت زیر تعریف می‌شود:

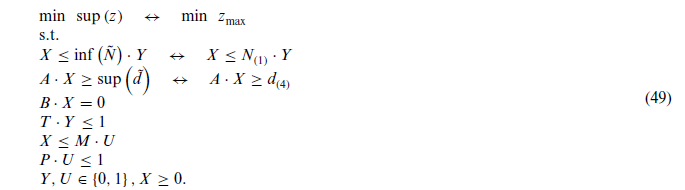مهم‌ترین مزیت این رویکرد این‌ است که به تابع توزیع امکان پارامترهای غیرقطعی نیاز ندارد اما از طرف دیگر پایین‌ترین سطح استواری بهینگی را در بین مدل‌های ارائه شده دارد.

اجرا و ارزیابی مدل:

به‌منظور ارزیابی سودمندی و عملکرد الگوهای پیشنهادی در یک مطالعه موردی واقعی، شبکه خدمات درمانی برای منطقه جنوب غربی تهران طراحی شده است.

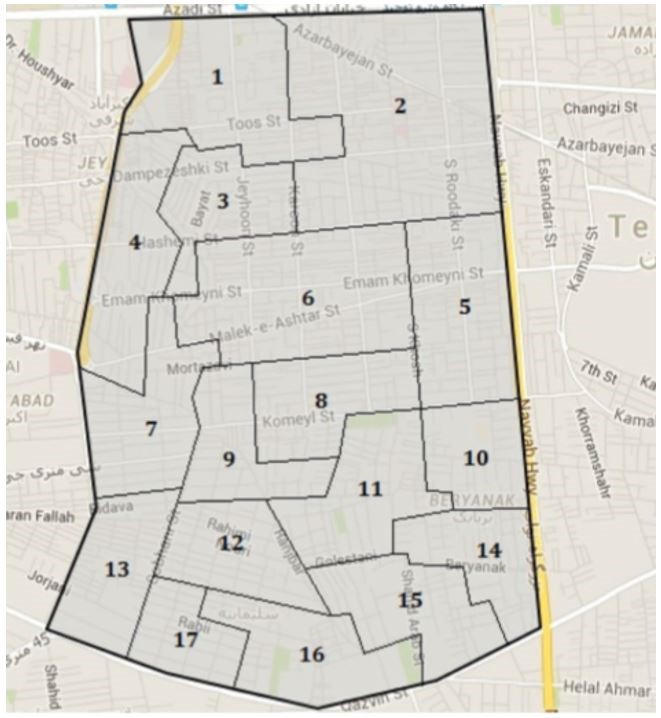
در کل 130 اجرا (یعنی 13 مدل هر کدام دارای 10 مجموعه داده تصادفی) انجام شد که نتایج آن در جدول1-1  نشان داده شده است.

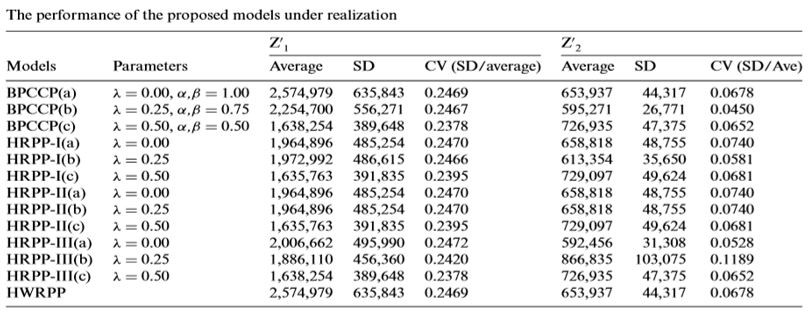
در بین مدل‌های پیشنهادی، مدل‌های HRPP-I (c) و  HRPP-II (c) از نظر میانگین و همچنین انحراف معیار و اندازه‌گیری  CV در رابطه با تابع  هدف اول بهتر، از مدل‌های دیگر هستند. با این حال، این مدل‌ها عملکرد ضعیفی در رابطه با تابع هدف دوم دارند. مدل HRPP-III (a)  از سایر مدل ها در مورد هدف دوم بهتر است. در مقابل، عملکرد قابل قبولی در رابطه با عملکرد هدف اول ندارد HWRPP و BPCCP(a)  بدترین عملکرد را در مورد تابع هدف اول و عملکرد متوسطی در رابطه با تابع هدف دوم دارند. نسخه های HWRRP و BPCPP (a) برای DM های کاملاً محافظه کار و ریسک‌گریز توصیه می‌شوند. در بین مدل‌های ارائه شده،  HWRPP و BPCCP به‌جز نسخه c دارای بدترین عملکرد در رابطه با انحراف معیار هستند. به همین دلیل است که استواری بهینگی و شدنی در تابع هدف آنها نادیده گرفته می‌شوند. اگر فقط تابع  هدف هزینه در نظر گرفته شود، HRPP-I (c) از انواع دیگر HRPP عملکرد بهتری دارد. اگر DM فقط نسبت به انحراف تابع هدف از مقدار بهینه مورد انتظار حساس باشد HRPP-II (c) بهترین عملکرد را در بین نسخه های مختلف مدل HRPP-II دارد، استفاده از HRPP-II (c) برای مطالعه موردی تحقیق پیشنهاد می‌شود.